応力特性曲線法はすべり線法とも呼ばれますが、以前から地盤の支持力や土圧・斜面安定問題などを検討する目的で広く用いられてきました。具体的には、下式に示した応力のつり合い式と降伏規準式を基に数値計算していくことで解を得ることができます。ただし、すべり線が一点に集中する「特異点」周りの処理など独特なテクニックを要することもあり、少し「とっつきにくい」面もあるかと思います。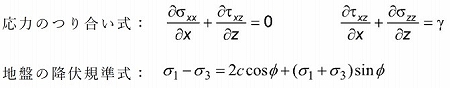

　ここでは、応力特性曲線法を目的とした解析プログラム「ABC - Analysis of Bearing Capacity」⁽¹⁾を用いて、剛な直接基礎の支持力について簡単な試計算を行ったので報告します（図-1）。

【計算条件】

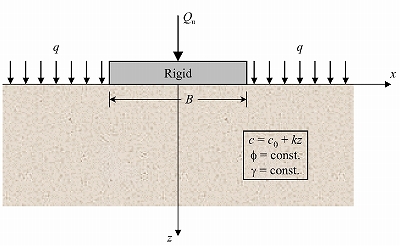
図-1　計算モデルの概要

　地盤定数：粘着力　　　 ｃ＝c₀＋k・z＝50＋5・z　(kN/m²)　（強度増加率m≒0.33）
　　　　　　内部摩擦角　 φ＝10　(°)
　　　　　　単位体積重量 γ＝15　(kN/m³)
　基礎底面：粗い・滑らか、の2ケース 　基礎形状：帯基礎（幅B＝3ｍ）、円形基礎（直径3m）
　押え荷重：q＝10　(kN/m²）

【計算結果】
　図-2に、基礎底面が滑らかな帯基礎のすべり線網を示します。すべり線網は基礎中央において左右対称なため、片側のみを表示しています。なお、基礎底面が粗いケースでは、基礎直下の主働領域でのすべり線網は省略されています。円形基礎は、平面ひずみモデルである帯基礎とは異なり軸対称モデルであることから、数値解法のプロセスが両者で若干異なります（円周方向に発生する地盤応力σ_yyが拘束圧として新たに考慮されます）。
　図-2より、基礎底面が粗い場合は滑らかな場合に比較して、すべり線網の規模（例えば、基礎直下の主働領域の幅や深さ）が大きくなっており、底面の粗・滑が極限支持力値に影響を与える結果となっていることが認められます。

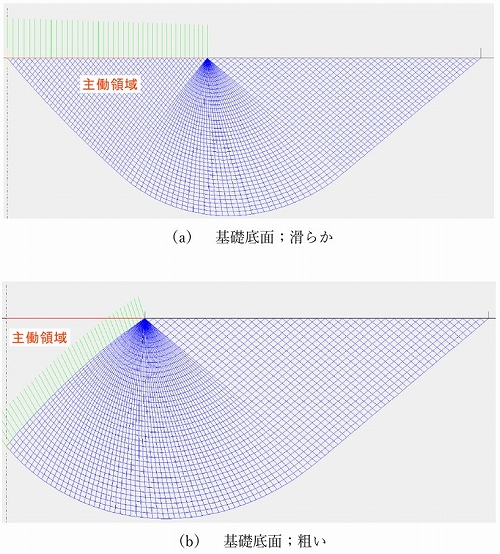
図-2　帯基礎のすべり線網

　図-3に、全ケースの極限支持力quについて計算結果をまとめました。図-3には、Terzaghiの支持力式（建築基礎構造設計基準、日本建築学会）による計算結果も併せて示しています。Terzaghiの支持力式では、強度増加率m=0の場合においてqu＝446kN/m²（帯基礎）、527kN/m²（円形基礎）となり、応力特性曲線法による計算結果に比べて15％程度小さな極限支持力が得られていることが認められます。この差異は、両者の解析モデルの違いや地盤の強度増加率mの考慮の有無などに起因しているものと考えられます。ちなみに、基礎幅が大きくなるとすべり線が地盤深部に及ぶことになるため、極限支持力に与える強度増加率mの影響も大きくなることに留意することが設計上、重要となります。

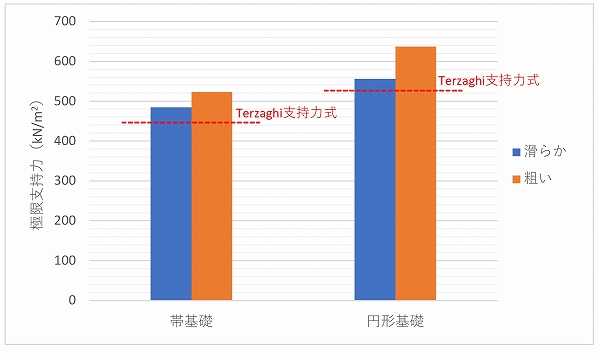
図-3　極限支持力quの計算結果

【参考文献】

（てこ）