FEMにおいて回転変形はラジアンで入力することになるのですが、この回転変形を入力する際に微小変位と大変形での違いに注意が必要です。

ラジアンについて
　まずラジアンについての説明ですが、角度の単位であり、半径の長さに対する円弧の長さの比を表しています。すなわち半径が1に対して円弧の長さが1になる角度が1ラジアンとなります。さらに半径rの円の円周は2πrですから2πr／r＝6.28ラジアン＝360°となります。

微小変位について
　FEMにおける線形解析では通常、微小変位である仮定の計算を行っています。解析による変形量はごく小さいものとして剛性変化、座標変化はなく、釣り合い計算を行った結果を算出します。具体的な例として、下の図は線を僅かな角度θだけ回転させたものになりますが、円弧の長さθL≒直角方向の変形量⊿Yとなります。なので、微小変位であれば角度は直角として変位を計算します。
　この微小変位の仮定による回転変形について、以下で実際に解析を行い見ていきます。

解析モデル
　・モデルは5パターン作成
　・２節点間を剛梁要素で接続
　・２節点の距離L=1.0m
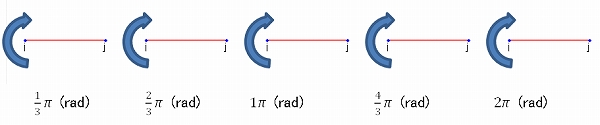
　・左側の節点i端を固定とし、回転強制変位θを入力（π/3～2πラジアン）
　・右側の節点j端はフリー
　・解析ケースは線形解析（微小変位）と幾何非線形解析（大変位）の2ケース

解析結果
　荷重ケース1線形解析（微小変位）
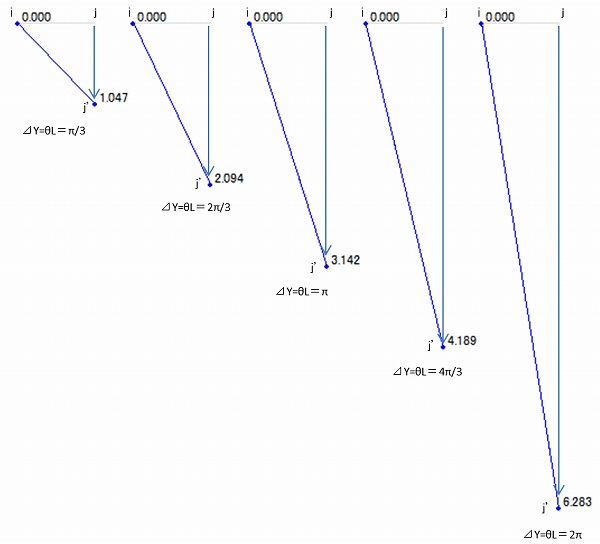
　解析結果（変形図）を示します。
　グレーの線（i-j）が変形前で青線（i-j’）が変形後の線です。
　数値は節点の変形量を示しています。
　荷重ケース2幾何非線形解析（大変位）
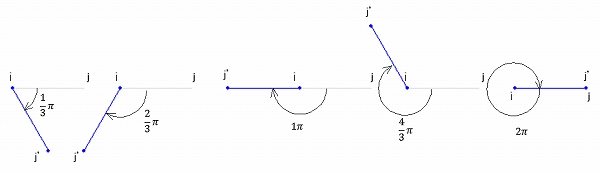
　解析結果（変形図）を示します。
　グレーの線（i-j）が変形前で青線（i-j’）が変形後の線です。

まとめ
　以上のように線形解析では回転の変形量は入力する変形量の大小にかかわらず直交方向にのみ出ることになりますが、幾何非線形解析では回転による節点の移動を考慮するため実際に回転させた形状になります。これらの結果においてどちらが正しいということではなく、微小変位、大変位という仮定を理解した上での解析を行っていればどちらも正しいこととなります。