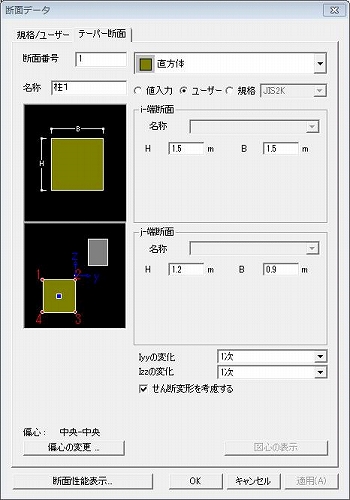
構造物をモデル化する際にテーパー断面梁要素を利用すると、さまざまな形状を実物と同じに表現することができて非常に便利です。また、テーパー断面梁要素の体積、重量についても自動で計算してくれます。
　今回はこのテーパー断面機能を用いて作成した梁要素と、同じ形状をソリッド要素によって作成したモデルについて、重量を比較、検証してみたいと思います。
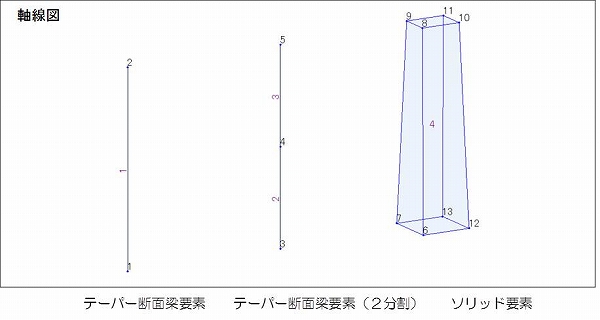
　ここでは下図に示すように、下端（i端）1.5m×1.5m、上端（j端）1.2m×0.9mの断面を有する高さ6.0mのテーパー付きの梁をモデル化してみました。左からテーパー断面でモデル化した梁要素、テーパー断面でモデル化した梁要素を２分割してテーパー断面グループとしたもの、ソリッド要素で全体をモデル化したものです。

　さて、ここでモデルの境界条件は下端固定とし自重解析を行います。ソリッド要素の下端は１節点で支持させるため、他の３節点を１節点に剛体連結しています。
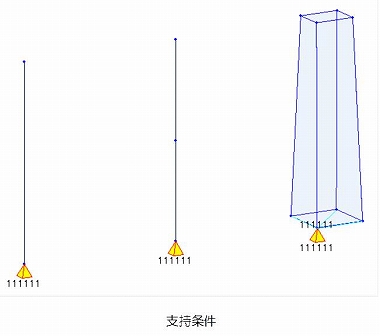
　結果の反力値を下図に示します。 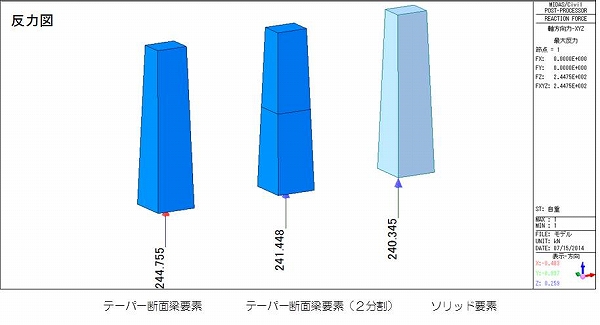　おや？反力値が異なります。体積はすべて同じはずですが、なぜでしょうか？
　手計算で重量を計算してみましょう。四角錐台の体積はオベリスク公式により、底面の辺長をA,Bとし、上面の辺長をa,b、高さをHとすると、
　V＝(Ab＋aB＋2(ab＋AB))×H／6
　　＝(1.5×0.9＋1.2×1.5＋2×(0.9×1.2＋1.5×1.5))×6.0／6
　　＝9.81m³
　単位重量を24.5kN/m³とすると重量Wは
　W＝V×γ＝9.81×24.5＝240.345 kN
　となります。

　ということは、ソリッド要素は正しく重量が算出されているようです。
　ではテーパー断面梁要素はというと、実はテーパー断面は単純な形状ばかりではないため、midasCivilでは、上面の断面積（S1）と下面の断面積（S2）の平均断面積×高さにより体積を算出するシステムになっています。
　すなわち、
　V＝(S1＋S2)×H／2
　で体積を計算しているため、１要素の場合は、
　V＝(1.2×0.9＋1.5×1.5)×6.0／2
　　＝9.99m³
　W＝9.99×24.5＝244.755 kN
　となります。

　これは底面と下面が相似形状の場合の角錐台の体積公式
　V＝(S1＋S2＋√(S1S2))×H／3
　とも異なるので注意が必要です。ちなみにオベリスク公式の体積は、上面と底面の形状が相似であれば上記角錐台の体積に一致します。

　ここで、反力図を見ると、２要素に分割した場合の反力のほうが、ソリッド要素に近い値となっています。これは積分の考え方と同じで、細かく分割してやればより正解に近づきます。上の例では３～４分割すると、ソリッド要素の結果にほぼ一致します。
　よって、テーパー断面梁要素においても厳密に重量を考慮したい場合には、テーパー断面グループを用いてある程度細かく要素分割した方がよいでしょう。