トンネルの覆工コンクリートは、主に掘削された地山のゆるみ荷重や、グラウンドアーチの応力解放に伴う発生荷重等を負担するために施工されます。覆工の厚さ(巻厚)は通常20～40cm程度で、場所打ちコンクリートで造られますが、施工後若材齢で型枠が取り外されるのが一般的です。型枠の脱型時期の目安は、柱、梁等の側枠で圧縮強度が5.0N/mm2以上とされていますが、覆工コンクリートの場合、さらに短時間で脱型されます。
そこでmidasCivilによって、施工後に覆工コンクリートに発生する応力度を計算し、許容応力度と比較することによって型枠脱型時期を検討してみました。
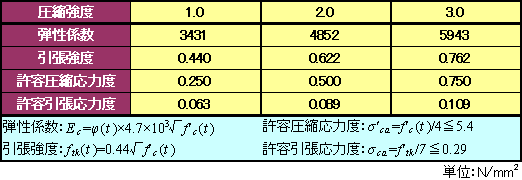
まず、若材齢におけるコンクリートの物性値は、表１のように圧縮強度を３通り仮定し、コンクリート標準示方書に基づいて算定しました。ここで許容応力度は無筋コンクリートのものです。
表１ コンクリートの物性値と許容応力度
次に解析モデルですが、ここでは図１に示すような形状の覆工コンクリートを考えます。CADの図面があれば、DXFファイルで保存しておけばmidasCivilでそのまま梁要素として読み込むことができます。また、覆工コンクリートの巻厚を30cmとし、単位奥行き（1.0m）あたりについて計算するものとして、梁要素の断面形状を高さ0.3m、幅1.0m（図２）とします。さらに、弾性係数は表１のとおり設定し、コンクリートの単位体積重量は23.5kN/m3としています。
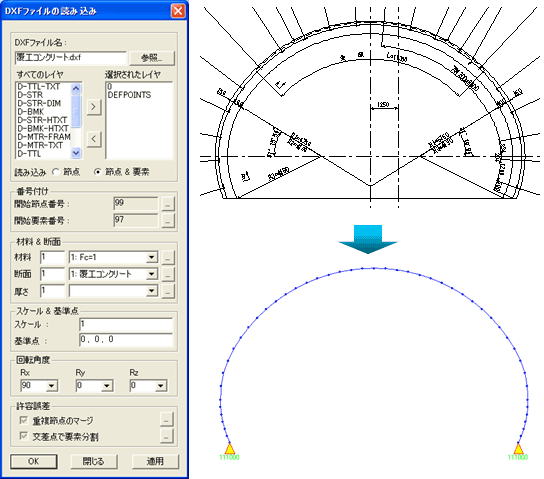
図１ DXFファイルの読み込みとモデル形状
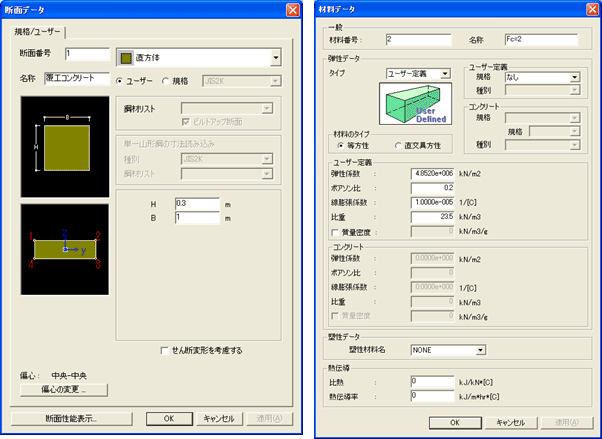
図２ 断面と材料データの設定
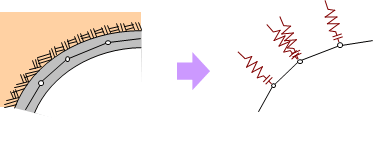
図３ 地盤ばねのモデル化
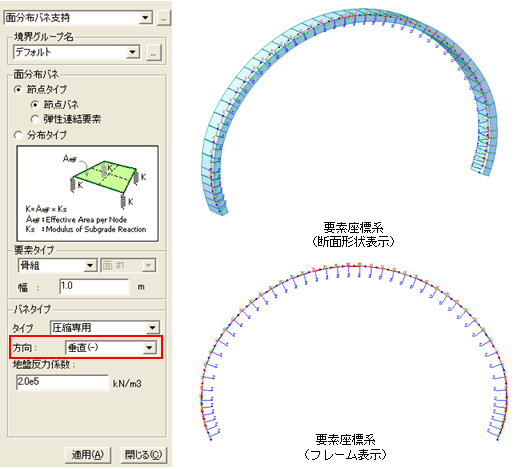
図４ 面分布ばねの設定
解析結果として、圧縮強度Fc=2.0N/mm2の場合の変形図、軸力図、モーメント図を図５に示します。これより断面力がわかりますから、通常であれば軸力とモーメントによる組合せ応力度が、最大（あるいは最小）となる位置において、許容応力度以下であることを次式により確認すればよいことになります。
σ＝N／A±Ｍ／Ｚ≦σa
σ：応力度
Ｎ：軸力
Ａ：断面積
Ｍ：曲げモーメント
Ｚ：断面係数
σa：許容応力度
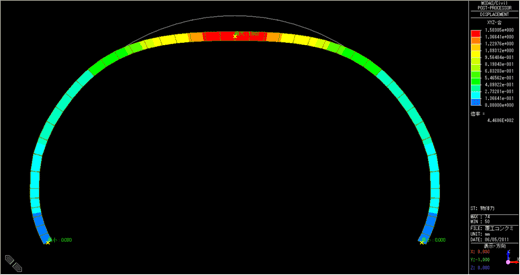
変形図
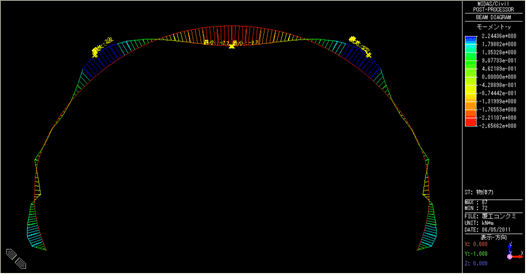
モーメント図
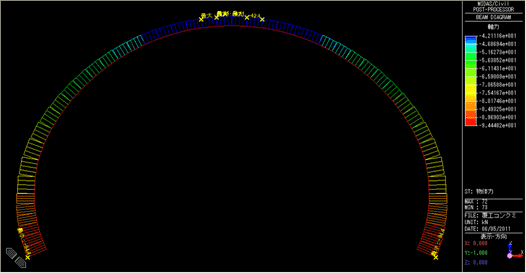
軸力図
図５ 解析結果（Fc=2.0N/mm2）
ところでmidasCivilは要素の軸応力度、せん断応力度、曲げ応力度、および組合せ（曲げ＋軸力）応力度をそれぞれ出力することができるので、断面力から発生応力度を計算しなくても、直接最大（最小）応力度を確認できます。図６はFc=2.0N/mm2の場合の組合せ（曲げ＋軸力）応力度の出力です。それぞれ断面の上縁と下縁の結果を示していますが、断面の上下は先程の要素座標系の通りなので、＋Ｚ側すなわち内空側が断面上縁となります。
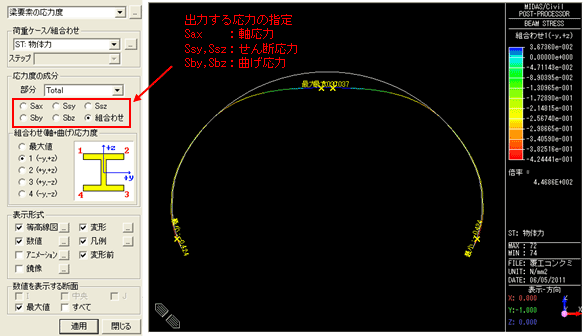
断面上縁（内空側）
断面下縁（地山側）
図６ 組合せ応力度の出力（Fc=2.0N/mm2）
さて、このようにして算定した各ケースにおける最大（最小）応力度と許容応力度の一覧を表２～表３にまとめました。応力度は圧縮が負、引張が正で出力されますが、表には絶対値で示しています。これより圧縮強度が2.0N/mm2以上であれば脱型可能であることがわかります。
表２ 圧縮応力度照査結果
表３ 引張応力度照査結果
最後に所定の圧縮強度に達するコンクリートの材齢の目安をコンクリート標準示方書を参考に次式により求めてみました。中庸熱ポルトランドセメントの場合、結果は表５のようになります。
表4 定数a,b,dの値
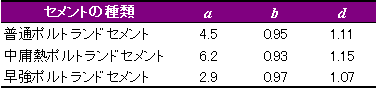
表５ 型枠脱型時のコンクリート材齢の目安
