1. はじめに
　前稿では，DIANAによる疲労破壊解析（FatigueFailureAnalysis）を実施し，手計算により算出した疲労寿命の理論値とほぼ一致する結果が得られることを示し，当該手法の有効性を検証した．本稿では，より複雑な実物構造物を対象として疲労寿命を評価する．
　鋼床版は，デッキプレート・縁板・Uリブなどを一体的に溶接して構築され，車両輪荷重を直接支持する構造であるため，高い疲労耐久性が要求される^1~3)．日本では，昭和55年の道路橋示方書改訂以降，許容応力度の設定および疲労設計の導入により，一定の安全性が確保されてきた．しかし近年，大型車両の交通量増加に伴い，Uリブとデッキプレートの溶接ルート部からプレートを貫通する「デッキ進展き裂」被害が全国的に多発しており，従来の設計細目や疲労寿命予測手法の妥当性が改めて問われている．
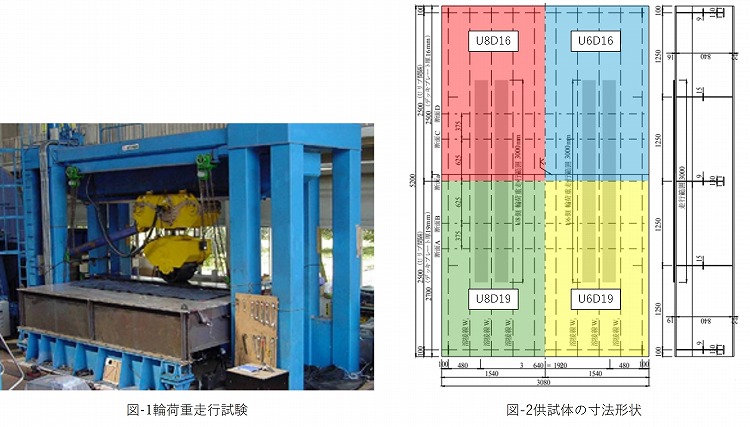
　本稿では，図-1に示すように，構造物メンテナンス研究センターが平成24年度に実施した実大試験体を用いた輪荷重走行試験^4,5）（以下，「走行試験」と呼ぶ）の結果を参照する．汎用有限要素解析システムDIANAによる疲労破壊解析を行い，解析モデルの妥当性を検証した上で，累積損傷則に基づいて各構造部位の疲労寿命および損傷分布を評価する．

2.鋼床版の疲労評価及び輪荷重走行試験
　図-2には，構造物メンテナンス研究センターで用いられた試験供試体の寸法形状を示す．デッキプレート厚は19mm（以下，D19）および16mm（以下，D16）の2種類とし，各デッキプレートにUリブ板厚6mm（以下，U6）および8mm（以下，U8）を各2本，計4本溶接した．試験対象とした構造形式はU6D16，U8D16，U6D19，U8D19の4組み合わせである．走行範囲は橋軸方向3000mm（片側1500mm），総輪荷重150kNとし，上記4ケースについて輪荷重走行試験を実施した．また，供試体のディテールは，「道路橋示方書・同解説II鋼橋編」および「鋼道路橋の疲労設計指針」に準拠して設計されたものである．

3.輪荷重走行試験の再現解析
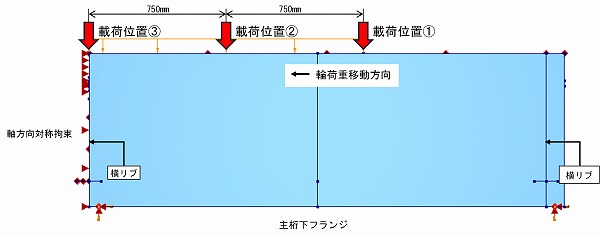
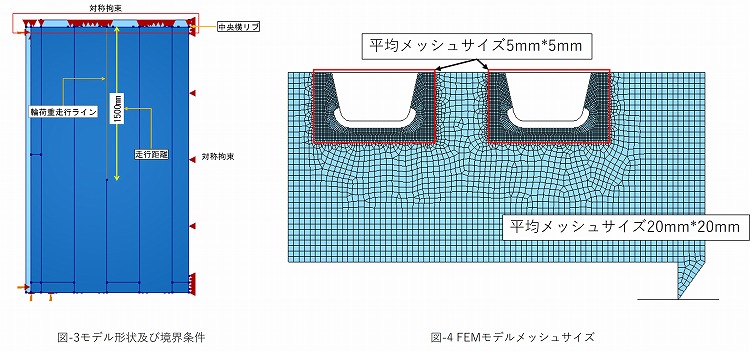
　本稿では，解析コストの低減を目的として，図-3に示す走行試験供試体の1/4モデルを採用した．橋軸方向および橋軸直角方向に対して対称境界条件を与え，主桁下部フランジの節点を全自由度拘束とすることで，実構造の幾何学的対称性を維持しつつ解析領域を1/4に低減した．
　解析モデルの妥当性検証および橋軸方向載荷位置の影響評価にあたっては，走行試験と同一の荷重条件を与え，1/4モデルの中央横リブ位置を基準点として，橋軸方向1500mmの範囲で輪荷重を移動載荷した．この設定により，実験で観測された応力およびひずみ分布と直接比較することが可能となる．
　横リブ，デッキプレート，Uリブの溶接接合部における局所的な応力集中および疲労損傷を高精度に再現するため，DIANAの自動メッシュ生成機能を用い，図-4に示すよう中央横リブとUリブ接合部周辺ではメッシュサイズを5mm×5mmに細分化し，それ以外の領域では20mm×20mmとした．

図-5 FEM解析における載荷位置及びひずみ結果output

図-6 ひずみ影響線実験vs.解析(橋軸中央から1000mm)

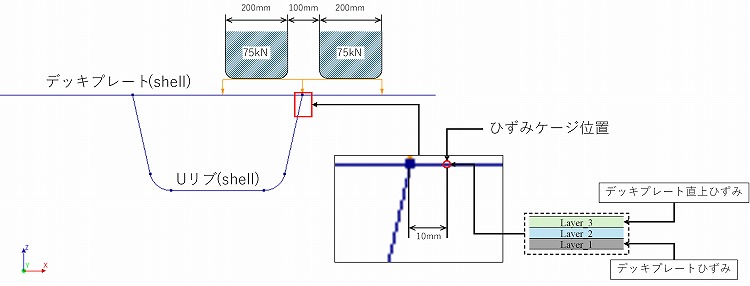
　材料物性値として，鋼材の弾性係数をE=206000N/mm²，ポアソン比をν=0.30とし，線形弾性体として取り扱った．さらに，本解析では解析コストの低減を図るため，部材は全てシェル要素でモデル化した．また，試験で測定されたデッキプレート直上および直下のひずみは，図-5に示すように厚さ方向三層分割シェル要素を用い，解析モデルにおける対応節点のLayer-1（下面側）およびLayer-3（上面側）のひずみと対応させている．
　図-6には，輪荷重走行時のひずみ影響線について，試験結果と解析結果を比較して示す．4ケース（U6D16，U8D16，U6D19，U8D19）におけるひずみ最大値の平均誤差は約10%であった．この誤差は，主としてシェル要素による板厚方向挙動の近似的なモデル化に起因すると考えられる．一方，ひずみ影響線の変動傾向およびピーク位置は，いずれのケースにおいても実験結果と良好な一致を示しており，ひずみ分布形状も概ね整合している．以上より，本稿で構築した有限要素モデルは，走行試験の挙動を適切に再現し得ると判断される．

図-7 疲労破壊曲線

4.疲労破壊解析
　疲労破壊曲線（S–N曲線）の定義および設定方法は前稿に示した．日本では昭和49年に，日本鋼構造協会が一般鋼構造物を対象として「日本鋼構造協会疲労設計指針・同解説（案）」（JSSC,Vol.10,No.101,1974.5）を策定している．同指針は主として軟鋼を対象とし，継手に疲労亀裂が発生しないことを前提としている．本稿では，図-7(a)に示すように鋼部材の疲労等級をAと仮定し，同図(b)に示す修正マイナー則を用いるS–N曲線を設定した．

図-8 載荷位置

図-9 解析コンター図

　図-8に輪荷重載荷位置の概要を示す．また，車輪(載荷位置)が中央リブから①1500mm，②750mm及び③0mmの位置における，鉛直変形及び最大・最小主応力コンターを図-9に示す．DIANAでは，荷重作用下における各節点の最大主応力と最小主応力の差を応力振幅とみなし，設定したS–N曲線に基づいて各節点の疲労寿命を評価する．

図-10 疲労寿命評価位置

　ここで，解析上局所的な応力集中現象は避けられないため，特定要素或は節点の疲労寿命のみを代表値とすると，疲労寿命を過小評価するおそれがある．ここではこの問題を緩和するため，図-10に示すとおり，各評価位置周辺から複数要素を抽出し，それらの疲労寿命の平均値を代表値として評価した．
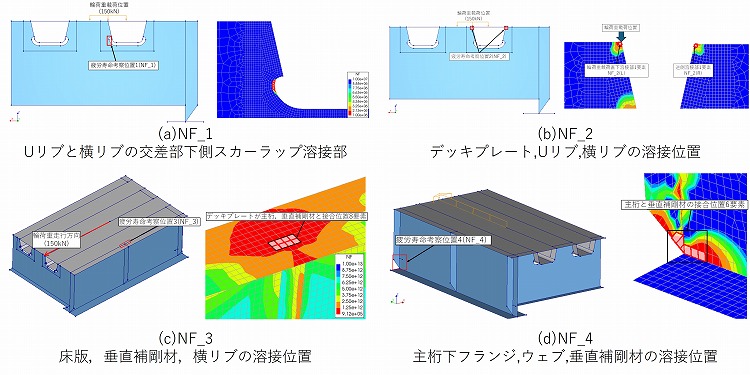
　評価位置(着目点)はNF_1〜NF_4の4か所とした．NF_1は輪荷重直下に位置するUリブと横リブの交差部下側スカーラップ溶接部である．NF_2はデッキプレートがUリブおよび横リブに溶接される位置であり，輪荷重直下側をNF_2(L)，輪荷重載荷位置から離れた側をNF_2(R)として区別した．NF_3は解析モデル中間位置に配置した垂直補剛材とデッキプレートおよび横リブとの溶接部であり，NF_4は主桁下フランジと主桁ウェブおよび中央垂直補剛材との溶接部である．これら4位置について，周囲の複数要素における疲労寿命の平均値を評価した．

　ここでは，U6D16の結果を基準値100%とし，他の解析ケースにおける平均疲労寿命の変化率を表-1に示す．4ケースの解析結果において，最も疲労寿命が短かった位置(着目点)は，Uリブと横リブの交差部下側スカーラップ溶接部であるNF_1(1.41E+06)であった．着目点NF_1において，デッキプレート厚をD16からD19(U6D19)に，あるいはUリブ板厚をU6からU8(U8D16)に増加させることで，疲労寿命はU6D16に対して，共に約1.7倍(2.40E+06)となり，両者を同時に厚板化したU8D19では，U6D16に比べて，疲労寿命が約2.6倍(3.68E+06)となった．以上より，厚板化による疲労寿命向上効果が確認された．
　つぎに，デッキプレートがUリブおよび横リブに溶接される位置NF_2の疲労寿命を評価する．4ケースとも，輪荷重直下側NF_2(L)よりも反対側NF_2(R)の疲労寿命が短くなる傾向を示した．U6D16においては，NF_2(L)の疲労寿命(1.16E+09)はNF_2(R)の約2.2倍(5.25E+08)であるのに対し，厚板化したU8D19では，NF_2(L)の疲労寿命(4.93E+09)はNF_2(R)の約4.2倍(1.17E+09)となり，両者の寿命差はさらに顕著となった．これは載荷位置における応力振幅が必ずしも最大とならないことを示している．
　垂直補剛材上端の疲労損傷位置NF_3はUリブに直接接続していないものの，U6D16からU8D16へのUリブ板厚の増加した場合，NF_3位置における疲労寿命は約7%増加した．一方，U6D16からU6D19へデッキプレート厚板化により，疲労寿命が約10％低下する傾向が確認された．これらの効果が相殺された結果，Uリブとデッキプレートを同時に厚板化にしたU8D19は，NF_3位置における疲労寿命がU6D16と比較して殆ど変化しなかった．
　また，主桁下フランジと主桁ウェブおよび垂直補剛材との溶接部であるNF_4は，厚板化した部材（Uリブおよびデッキプレート）と直接接触していないにもかかわらず，U6D16からU6D19，U8D16，U8D19へと部材厚を増加させることで，疲労寿命が約3~8％向上した．これは，周辺部材の剛性向上により局所的な応力分布が改善されたためと考えられる．

5.結論
　本稿では，輪荷重走行試験の有限要素モデルによる再現解析を行い，その妥当性を確認したうえで，DIANAの疲労破壊解析機能を用いてデッキプレートおよびUリブの厚板化が鋼床版各部の疲労寿命に及ぼす影響を検討した．得られた主な知見を以下に示す．