逆対称曲げモーメントを受けるディープビームのせん断破壊シミュレーション
DIANA Tips 2023.10.031. はじめに
せん断スパン比が小さい(a/d=1.0~2.5程度)RC梁をディープビームと呼び,そのせん断破壊形態は支点と載荷点を結ぶ斜めひび割れの発生後,コンクリートが圧縮強度に到達するせん断圧縮破壊となります.
これまで「2017年制定 コンクリート標準示方書」や「平成16年4月 鉄道構造物等設計標準・同解説」にて算定されてきた設計せん断圧縮破壊耐力Vddは単純支持されたディープビームを想定していますが,実際の鉄道高架橋等に用いられるものは両端固定支持である場合も多く,その耐荷機構は単純支持のものと異なり,「令和5年1月 鉄道構造物等設計標準・同解説 第Ⅲ編コンクリート構造」(以後鉄道標準)では両端固定支持された棒部材の設計せん断耐力Vasudが新設されました.本コラムでは既往の実験結果1)の再現解析を非線形有限要素解析にて行い,実験結果と解析結果および鉄道標準に規定されている設計せん断耐力算出結果をそれぞれ比較し,その精度について検証を行います.
2. 解析概要
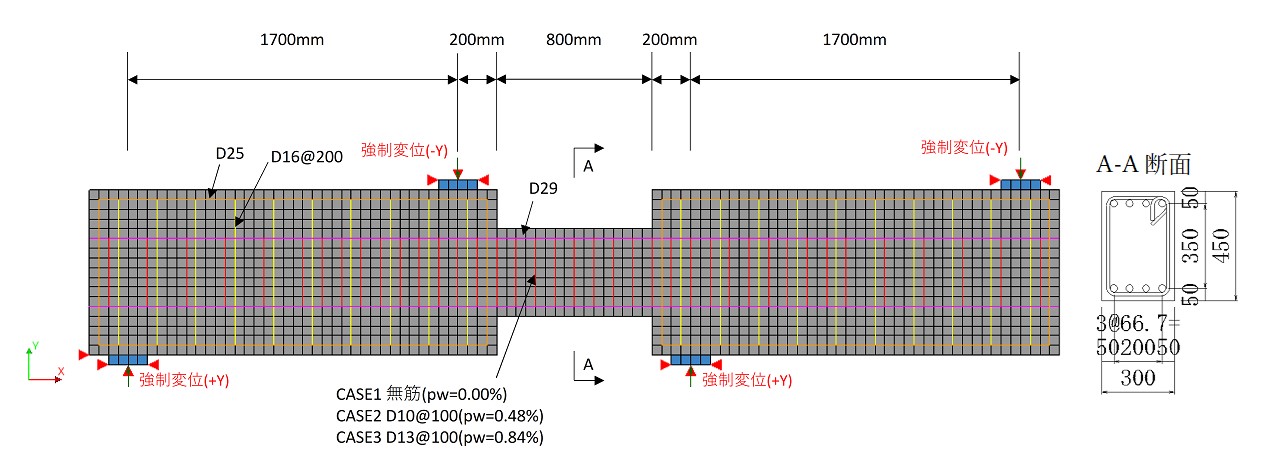
再現解析は二次元非線形有限要素解析を行いました.解析モデルは図1に示す両端部にフーチング部を有するa/d=1.0の矩形断面のRC梁であり,支間中央のせん断補強筋比pw=0.00%,0.48%,0.84%の3ケースについて検討を行いました.載荷方法は4点曲げ単調載荷とし,支間中央にて曲げモーメントの正負が反転する逆対称曲げモデルとなっています.コンクリートは分散ひび割れモデル,鉄筋は埋め込み鉄筋を使用した離散鉄筋モデルを用いてモデル化しました.コンクリートは一般平面応力要素(アイソパラメトリック二次要素)を用いました.鉄筋は完全付着としました.また,実験と同様に載荷点に応力集中を生じさせないため支圧版をモデル化し,フーチング部との接触面は水平ローラーとしました.また,解析ソフトはDIANA10.5(開発:DIANA-FEA社)を用いました.
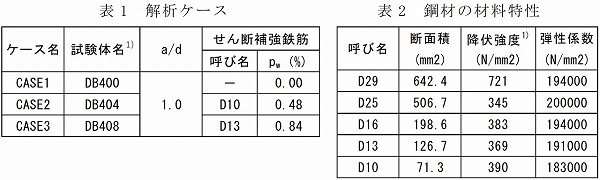
表1に解析ケースを示します.また,解析に用いた鋼材の材料特性を表2に,コンクリートの材料特性を表3に示します.コンクリートの引張強度はftk=0.23f’ck2/3,引張破壊エネルギーはGF=10(dmax)1/3・f'ck
1/3を用いて算出し,コンクリートの非線形特性はコンクリート標準示方書より設定しました.また,コンクリートのひび割れモデルは固定ひび割れモデルとし,せん断伝達モデルには前川による接触密度関数モデルを用いました.また,鉄筋の降伏基準はVonMisesとしました.
荷重は支圧版中央部にそれぞれ強制変位を与え,1ステップ0.03mmを150ステップ載荷しました.イタレーション法にはNewton-Raphson法を用い,収束判定はエネルギーノルム比0.001として解析を行いました.

3. 設計せん断耐力の算出
表1で示した各ケースについて,鉄道標準にて規定されている設計せん断圧縮破壊耐力Vdd
と,両端固定支持された棒部材の設計せん断耐力Vasudを算出した結果を表4に示します.
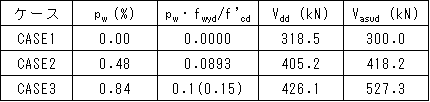
Vdd は載荷点と支点を結ぶ圧縮ストラットのコンクリートによるせん断耐力のため,せん断補強鋼材の影響は軽微となっています.一方,Vasudは修正トラス理論による算出式のため,せん断補強筋比が大きくなるにつれせん断耐力も大きくなりますが,せん断補強筋が降伏することを前提としているため,pw・fwyd/f'cd≦0.1の条件を満たす必要があります.(CASE3はこの条件を満たしていませんが,0.1を上回るものは0.1として計算して良いとされているため,0.1を用いてせん断耐力を算出しました)
4. 解析結果
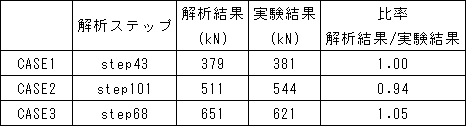
解析の結果得られた各ケースの荷重-変位曲線を図3に示します.また,それぞれの最大荷重を表5に示します.荷重-変位曲線では,解析結果は実験結果と比べると層間変位が小さいですが,最大荷重については全ケースで実験結果を精度よく再現できました.
(解析結果と実験結果1)の比較)
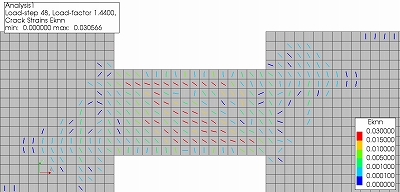
CASE1について,図4,図5にひび割れひずみコンターおよび最小主応力コンターのアニメーション、それぞれの最大荷重到達後のコンターを示します.
 |
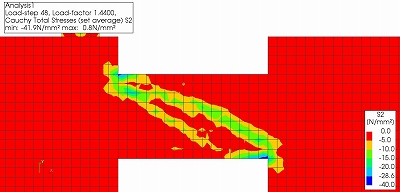 |
CASE1ではstep43にて最大荷重となり,最大荷重以後は図4,図5に示すように支間中央に斜めひび割れが発生し圧縮ストラットが形成できなくなり,図3に示すように急激に耐力が低下します.
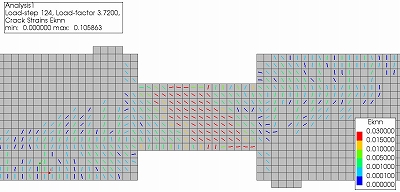
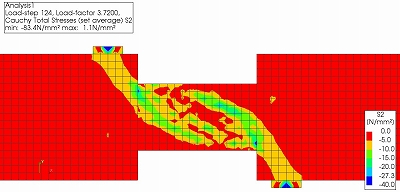
次に,CASE2について図6にひび割れひずみコンター,図7に最小主応力コンター,図8に正規化累加ひずみエネルギーコンターのアニメーションを示します.また,それぞれCASE3よりもせん断耐力が大きくなるstep124でのコンターを示します.
 |
 |
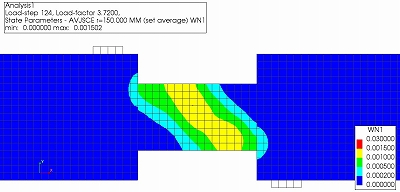 |
(平均化領域の半径2)=150mm)
CASE2では図6,図7,図8に示すように支間を対角に結ぶひび割れが発生した以降も圧縮ストラットを維持するため急激な耐力低下は起きませんでした.これはひび割れが支間全体に分散し,局所的な破壊が起きず,支間全体のせん断補強筋が応力を受け持つからだと考えられます.
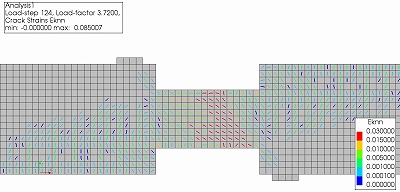
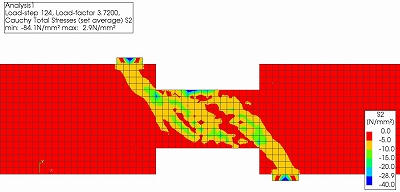
CASE3についても,同様に図9にひび割れひずみコンター,図10に最小主応力コンター,図11に正規化累加ひずみエネルギーコンターのアニメーションを示します.また,それぞれCASE2よりもせん断耐力が小さくなるstep124でのコンターを示します.
 |
 |
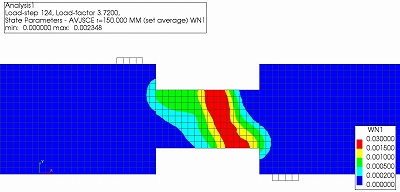 |
(平均化領域の半径2)=150mm)
CASE3では図9,図10,図11に示すようにひび割れが局所的に発生した以後,最終的に圧縮ストラットを維持出来なくなり,図3に示すように急激な耐力低下が起きています.CASE2と異なり局所的な破壊が起きた原因としては,せん断補強筋比が大きすぎるため,せん断補強筋の降伏より先にコンクリートのせん断圧縮破壊が進行しているためだと考えられます.
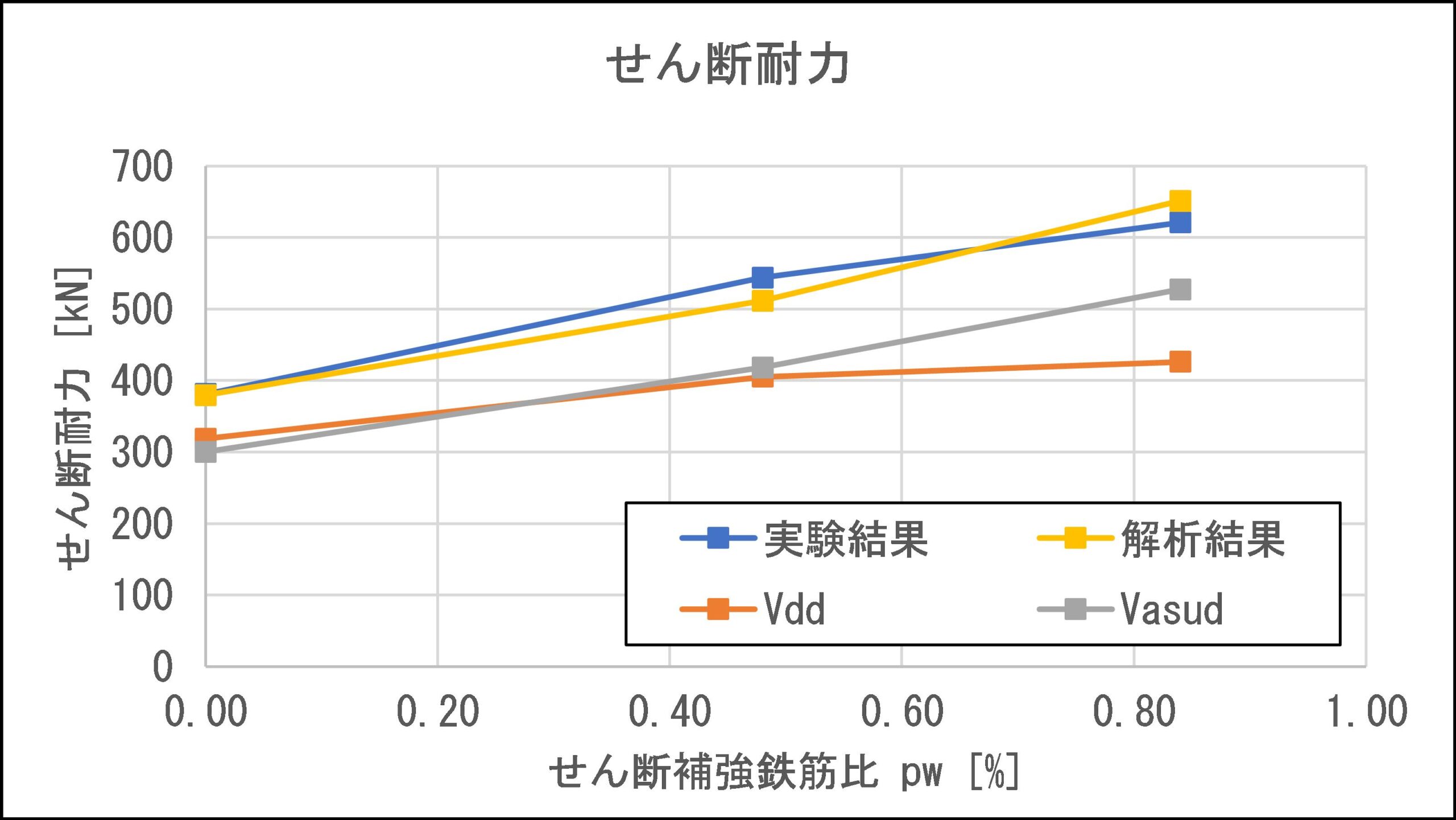
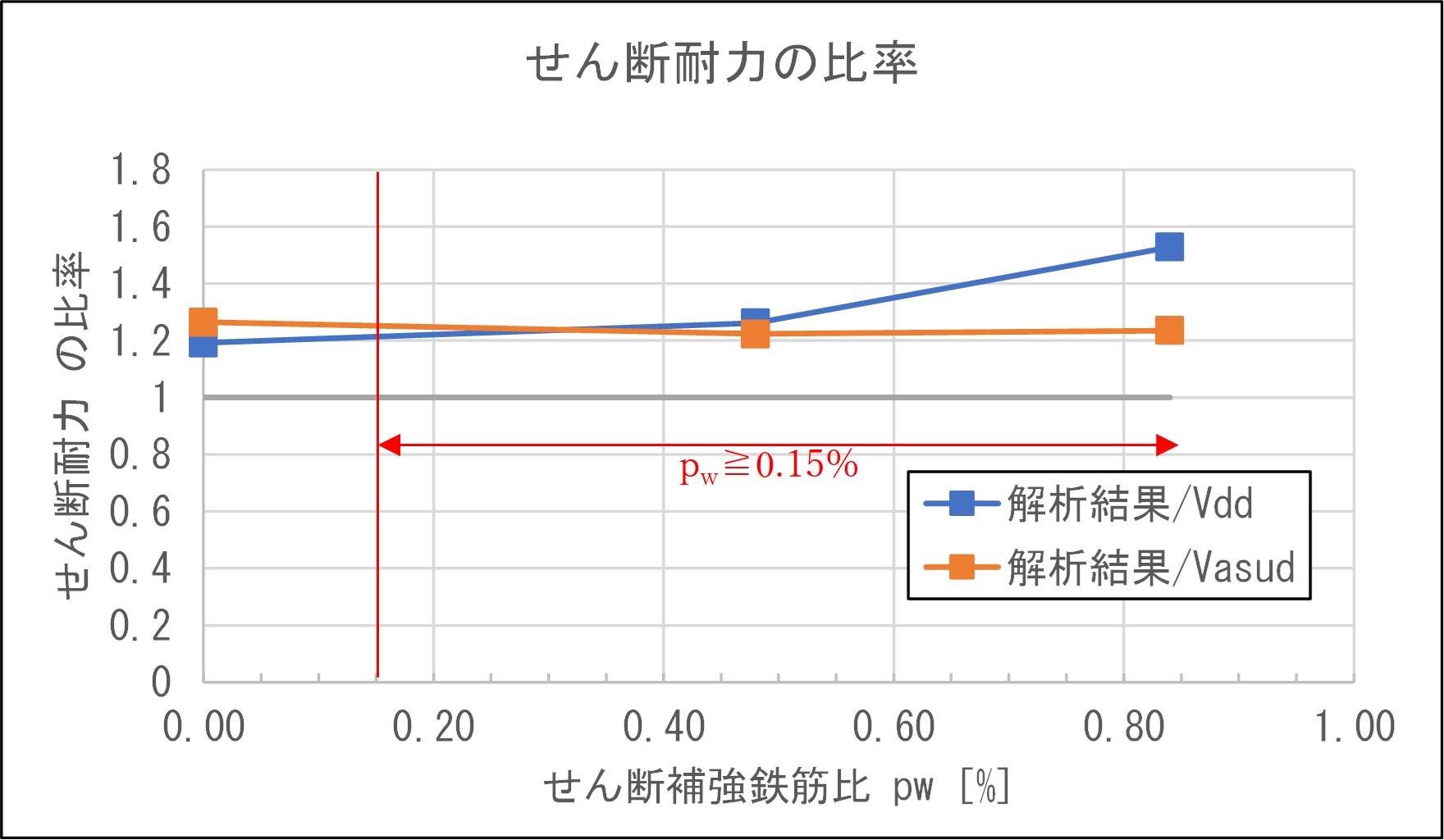
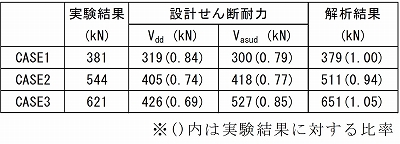
実験結果1),鉄道標準により算出した設計せん断耐力,解析結果を比較します.表6に各せん断耐力の一覧を示します.設計せん断耐力は実験結果,解析結果と比べ15~20%程度小さい値となっており,安全側の評価となっていることがわかります.また,図12に各せん断耐力のグラフを,図13に解析結果とVdd
,Vasudの比率をプロットしたグラフを示します.
Vdd
は前述の通りせん断補強鉄筋比の増加があまり耐力に影響しません.そのため,Vdd
の算出式を用いてせん断耐力を増やそうと過剰なせん断補強筋を配置することで逆にコンクリートのせん断圧縮破壊を招き,CASE3のような急激な耐力低下を引き起こしかねないため,注意が必要です.
また,図13からVasudの適用範囲とされている最小鋼材量pw≧0.15%の領域ではVasudの方がVdd
よりも解析結果と一致することがわかりました.
4. まとめ
令和5年に改訂された鉄道標準に新設されたVasudについて,既往の実験1)の再現解析結果と設計せん断耐力算出値の比較を行い,従来のVddと比べて精度よく一致することが確認されました.Vddを用いる場合,せん断耐力を増加させる目的でせん断補強筋比を大きくしてもコンクリートのせん断圧縮破壊を招くため,効果が期待できません.一方,VasudはVddと比べてせん断補強筋によるせん断耐力増加が見込めるため,最小鋼材量やpw・fwyd/f'cd≦0.1等の適用条件に注意は必要ですが,より合理的な設計が可能となります.
参考文献
コンクリート工学年次論文集,Vol.29,No.3,2007:渡辺健,田中敏弥,谷村幸裕,黒川浩嗣
土木学会論文集E2(材料・コンクリート構造),Vol.68,No.3,pp.209-22,2012:土屋智史,牧武史,斉藤成彦,渡邊忠朋,前川宏一