前回のコラムでは、斜面を対象としたせん断強度低減法の解析を行い、せん断強度低減法の全体安全率はFEMのメッシュサイズに依存し、メッシュサイズを小さくするほど円弧すべり法の結果に近づくことがわかった。また、最大せん断ひずみ分布もメッシュサイズを小さくするほど明瞭になることがわかった。
　今回のコラムでは、切土補強土工法を適用した場合でも前回と同様な結果が出るかどうかを調べた。

1.　切土補強土工法
　前回作成したモデルと同様のモデル形状に対して補強材を設置することで全体安全率がどのように異なるか調べた。

1.1　モデルの設定と円弧すべり法の結果
　設置する補強材の物性値（表-1）と前回のモデルと同様の斜面形状と地盤物性値（表-2）を設定し、そのモデルにおける円弧すべり法による計算を行い、その際の最小安全率と円弧を求めた（図-1）。 
　なお、補強材の周面摩擦抵抗力はせん断強度低減法のFEM解析モデルと合わせるため補強材が引抜けないよう大きな値とした。

表-1　補強材の物性値

表-2　地盤物性値

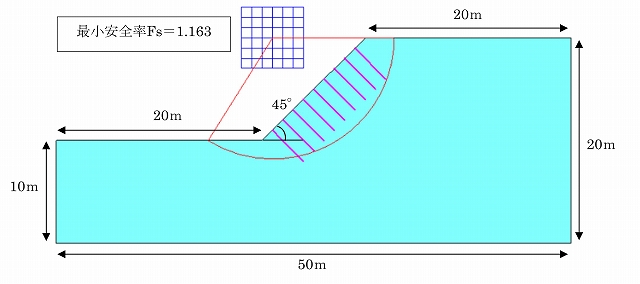
図-1　モデル図および円弧すべり計算の結果

1.2　メッシュサイズと補強材物性値
　FEM解析におけるメッシュサイズは前回と同様の3ケースとした。補強材を設置したメッシュ図を図-2～4に示す。また、補強材は埋込みトラス要素でモデル化しその物性値を表-3に示す。

表-3　せん断強度低減法に用いる補強材の物性値

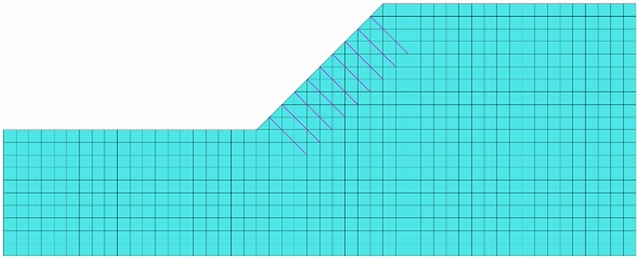
図-2　①1.0m×1.0mのメッシュ

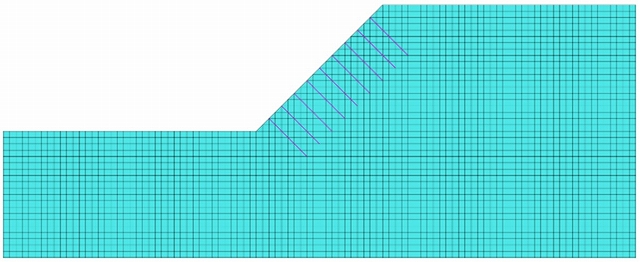
図-3　②0.5m×0.5mのメッシュ

図-4　③0.1m×0.1mのメッシュ

1.3　せん断強度低減法の結果
　せん断強度低減法の結果における各ケースの安全率を表-3に、最大せん断ひずみ分布を図-5～7に示す。
　①②のケースでは、補強のない場合と同様な結果となったが、③のケースでは最大せん断ひずみの大きい領域が補強材周辺に局所的に発生し、円弧のような形状が発生しなかった。

表-4　各ケースのFs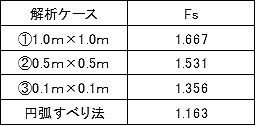

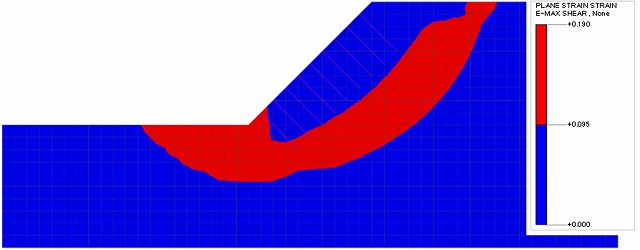
図-5　①1.0m×1.0mの最大せん断ひずみ図（Fs=1.667）

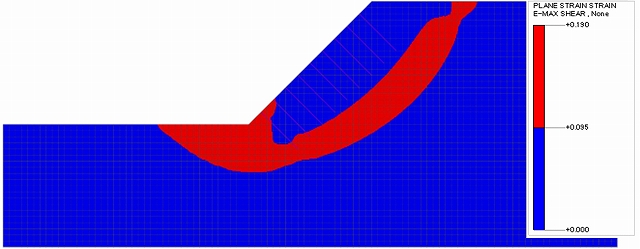
図-6　②0.5m×0.5mの最大せん断ひずみ図（Fs=1.531）

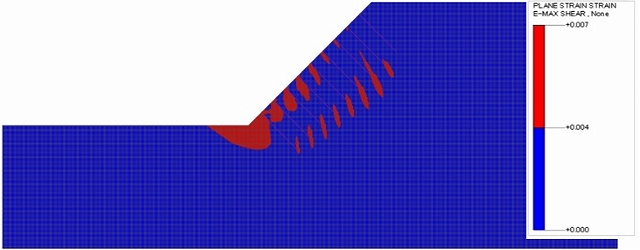
図-7　③0.1m×0.1mの最大せん断ひずみ図（Fs=1.356）

2.　切土補強土工法の補強範囲を弾性体とすることによる比較
　③のケースでは、最大せん断ひずみの大きい領域が補強材周辺に局所的に発生し、円弧のような形状が発生しなかった。そこで、補強材を打設した範囲を弾性体としてモデル化し、局所的に最大せん断ひずみが発生しないようにして解析を行った。

2.1　補強範囲のモデル化
　図-8～10の赤点で示した要素を弾性体とした。ここで、弾性体とした範囲は最大メッシュサイズの①のケースと同様になるようにした。

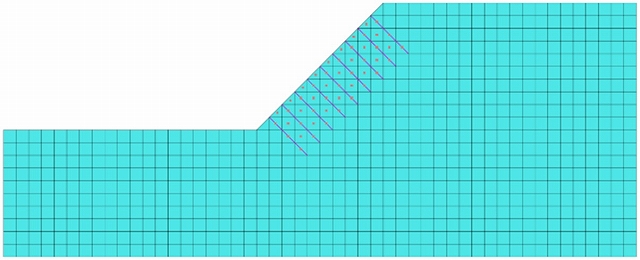
図-8　①1.0m×1.0mのメッシュ

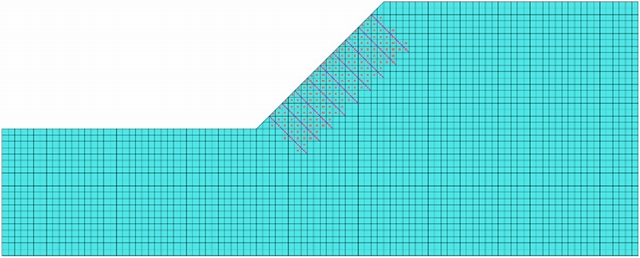
図-9　②0.5m×0.5mのメッシュ

図-10　③0.1m×0.1mのメッシュ

2.2　せん断強度低減法の結果
　せん断強度低減法の結果における各ケースの安全率を表-5に、最大せん断ひずみ分布を図-11～13に示す。
　①②のケースでは、補強範囲の地盤を弾性体としても安全率にほとんど差はなかった（図-11,12）。
　③のケースでは、補強範囲の地盤を弾性体とすることで、安全率は円弧すべり法の結果から遠くなった（図-13）。しかし、円弧すべり面が確認できたことから切土補強土工法の結果としては弾性体とした結果の方が妥当であると考える。

表-5　各ケースのFs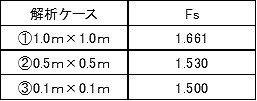

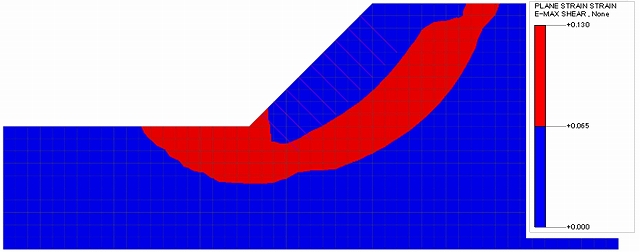
図-11　①1.0m×1.0mの最大せん断ひずみ図（Fs=1.661）

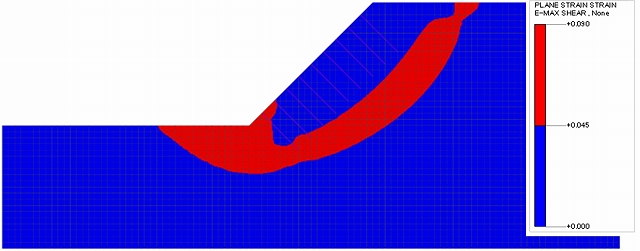
図-12　②0.5m×0.5mの最大せん断ひずみ図（Fs=1.530）

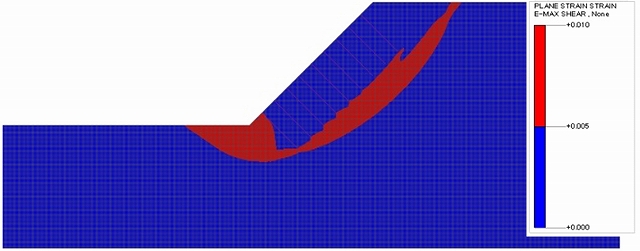
図-13　③0.1m×0.1mの最大せん断ひずみ図（Fs=1.500）

3.　まとめ
　補強土工法を適用した場合も概ね前回と同様な結果となることがわかった。ただし、メッシュサイズが小さい場合には、補強材をトラス要素でモデル化すると、最大せん断ひずみが局所的に大きくなり円弧形状にならない。その場合は、補強材をモデル化するのではなく、補強範囲を弾性体とするようなモデル化を行う必要がある。