CREATEC TECHNICAL BLOG
クレアテック技術ブログ
戻る
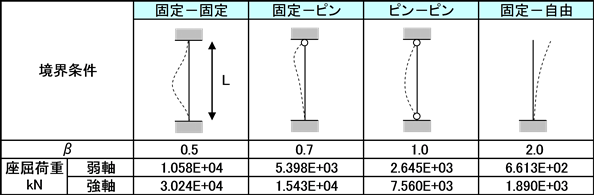
midasCivilの座屈固有値解析機能を用いて長柱の座屈荷重を求めてみました。対象としたのはH形鋼の規格材であるH100×100×6/8(図1)です。柱の諸元を表1に示します。モデルでは柱長さをL=1.0mとして、表2に示す境界条件を設定しました。表2には境界条件ごとに、断面の強軸方向および弱軸方向の臨界座屈荷重の理論値も併記しています。理論値であるオイラーの座屈荷重は次式で求められます。
Pcr=(π/βL)2EI
Pcr:座屈荷重
βL:有効座屈長
E:弾性係数
I:断面二次モーメント
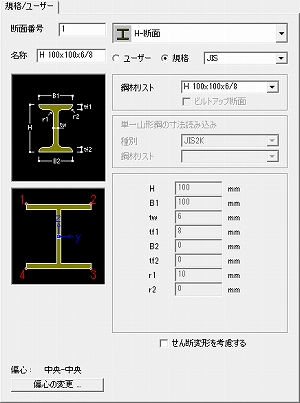 図1 H形鋼断面諸元
図1 H形鋼断面諸元
表1 柱諸元(H100×100×6/8)

表2 境界条件と座屈荷重の理論値
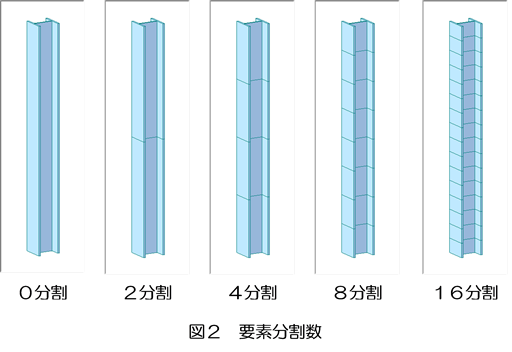
 さて、座屈固有解析では、その座屈モードを再現できる要素分割が必要になります。たとえば境界条件が「固定-固定」で要素分割がゼロ(梁1要素)の場合は座屈モードが再現できないため、エラーとなります。とうぜん要素分割を細かくすれば再現できる座屈モードの次数も多くなります。また分割数は座屈荷重の精度にも影響してきます。そこで、ここでは図2のように要素分割数をパラメータとして座屈固有値解析を行ってみました。
座屈固有値解析を行うためには、剛性マトリクスを構成するために、想定する荷重方向に静的荷重を与える必要があります。ここで単位荷重を与えておくと座屈荷重は臨界座屈荷重係数として出力されます。また、座屈荷重制御では計算する座屈モードの次数を与えておきます。
さて、座屈固有解析では、その座屈モードを再現できる要素分割が必要になります。たとえば境界条件が「固定-固定」で要素分割がゼロ(梁1要素)の場合は座屈モードが再現できないため、エラーとなります。とうぜん要素分割を細かくすれば再現できる座屈モードの次数も多くなります。また分割数は座屈荷重の精度にも影響してきます。そこで、ここでは図2のように要素分割数をパラメータとして座屈固有値解析を行ってみました。
座屈固有値解析を行うためには、剛性マトリクスを構成するために、想定する荷重方向に静的荷重を与える必要があります。ここで単位荷重を与えておくと座屈荷重は臨界座屈荷重係数として出力されます。また、座屈荷重制御では計算する座屈モードの次数を与えておきます。
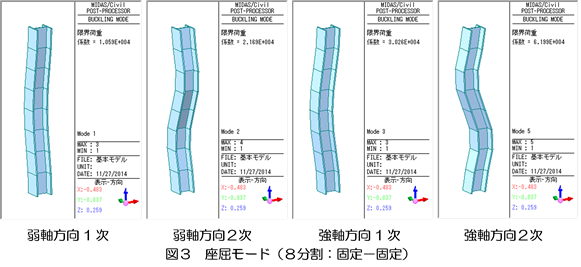
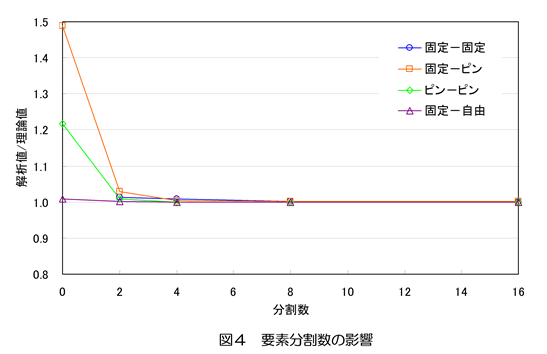
 座屈モードの出力例を図3に示しました。また、座屈荷重の一覧を表3に、要素分割数と理論値の比較を図4に示します。これによると境界条件によって異なりますが、8分割数以上とすれば理論値とほぼ一致します。
座屈モードの出力例を図3に示しました。また、座屈荷重の一覧を表3に、要素分割数と理論値の比較を図4に示します。これによると境界条件によって異なりますが、8分割数以上とすれば理論値とほぼ一致します。

 次に応用として、鋼管杭が半ば地中に設置されている状況を想定して臨界座屈荷重を求めてみます。杭は鋼管杭としてφ600、t=12mm、杭長10mのうち6mが地中にあるものとします。解析モデルを図5に示します。杭先端はピン支持として、地中部分には地盤反力係数を与えて地盤ばねを設定します。要素分割は20分割としています。
次に応用として、鋼管杭が半ば地中に設置されている状況を想定して臨界座屈荷重を求めてみます。杭は鋼管杭としてφ600、t=12mm、杭長10mのうち6mが地中にあるものとします。解析モデルを図5に示します。杭先端はピン支持として、地中部分には地盤反力係数を与えて地盤ばねを設定します。要素分割は20分割としています。
解析結果を図6に示します。座屈荷重は13290kNとなりました。図6には鋼管のみ(固定-ピン)の場合の座屈解析結果も併記しました。鋼管のみの場合の座屈荷重は4728kNなので、地盤の影響(弾性ですが)により座屈荷重が大幅に上昇したことになります。
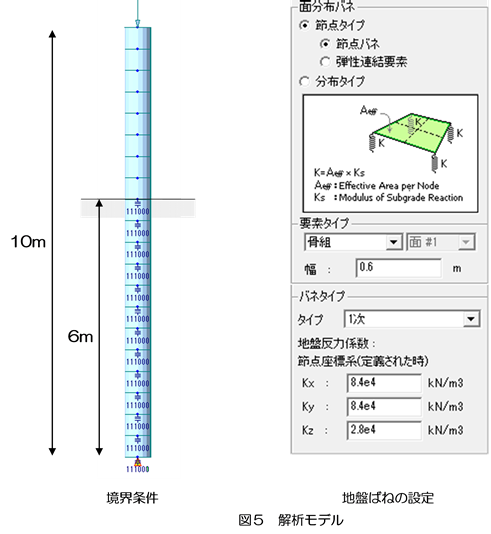
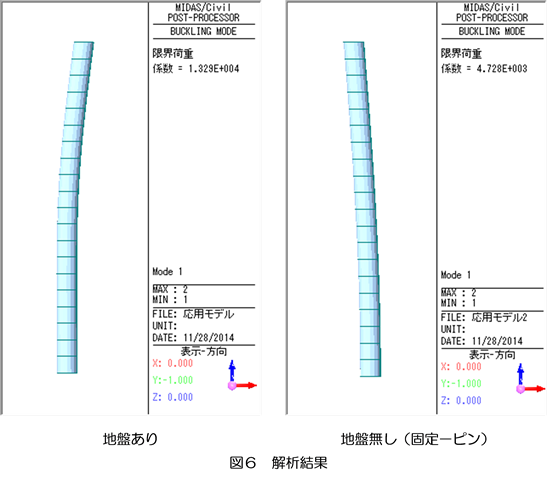
 図1 H形鋼断面諸元
図1 H形鋼断面諸元







 図1 H形鋼断面諸元
図1 H形鋼断面諸元






