盛土の安定検討
解析全般 2023.04.04 熱海の盛土崩落事故が起きてから盛土に対する安定性について気になることがあります。
そこで今回は「設計要領第一集 土工 建設編 4 高盛土・大規模盛土,NEXCO」(以下、「設計要領」)に示されている高盛土・大規模盛土の安定検討のうち、レベル2地震動における安定検討を実施し、地震後の盛土の残留変位量を計算してみたいと思います。
計算としては初期応力解析による拘束圧に応じた地盤の動的物性値を設定し等価線形解析を行います。次に円弧すべり面を設定し、すべり土塊に含まれる全節点の応答加速度を抽出し、すべり土塊の等価加速度(ニューマーク法における適用波形)を算出します。最後にニューマーク法に基づき、降伏震度を超える震度での等価回転加速度を積分し、すべり土塊の残留回転角(残留変位量)を算出します。
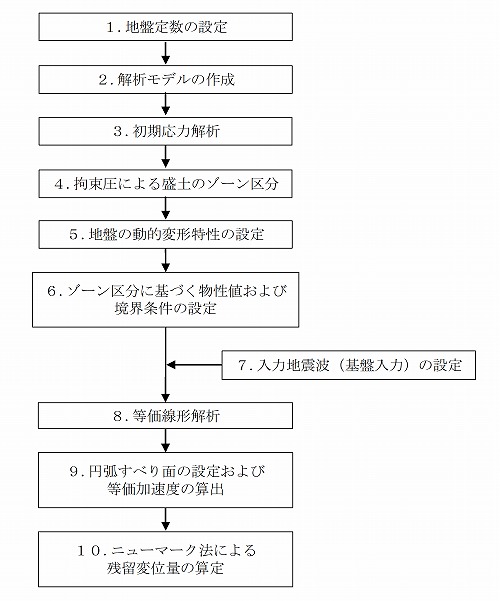
1.地盤定数の設定
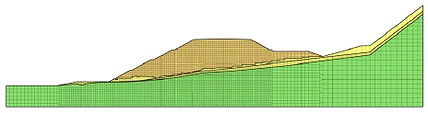
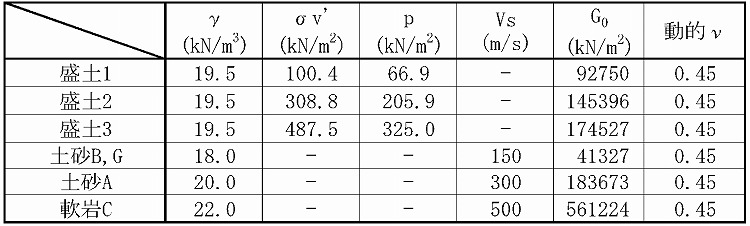
・検討断面は傾斜した不整形地盤上の高盛土(最大盛土高さ40m程度)を対象とする。
 ・盛土部(砂質土)における初期せん断弾性係数Goは、「設計要領」に示される砂質土の式より算出
・盛土部(砂質土)における初期せん断弾性係数Goは、「設計要領」に示される砂質土の式より算出
 ・原地盤(土砂,軟岩)の初期せん断弾性係数Goは、PS検層により得られているせん断波速度VSより算出
・原地盤(土砂,軟岩)の初期せん断弾性係数Goは、PS検層により得られているせん断波速度VSより算出
・初期応力解析における盛土の平均有効主応力pは、盛土中心での中央深度の値とする
平均有効主応力pは鉛直応力σvおよび静止土圧係数Koを用いた水平2方向の応力(σh1,σh2)との3方向応力の平均応力として求める
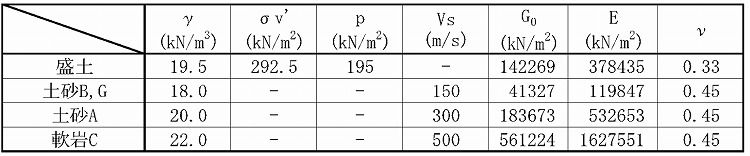
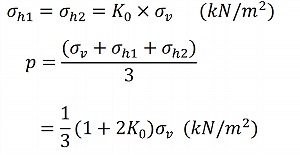 ・上記条件で設定した定数を下表に示す
・上記条件で設定した定数を下表に示す
2.解析モデルの作成
初期応力解析におけるメッシュ図を示す。
3.初期応力解析
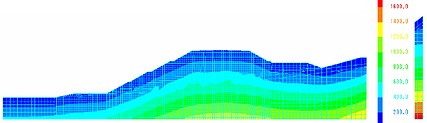
初期応力解析により得られた鉛直応力を示す。
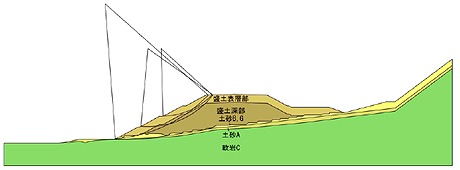
4.拘束圧による盛土のゾーン区分
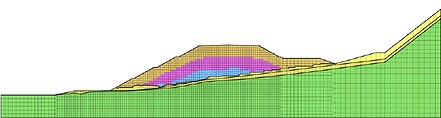
初期応力解析結果をもとにして、下図に示すように拘束圧p のレベルに応じて3つのゾーン(上部から順に盛土1、盛土2、盛土3)に区分した。
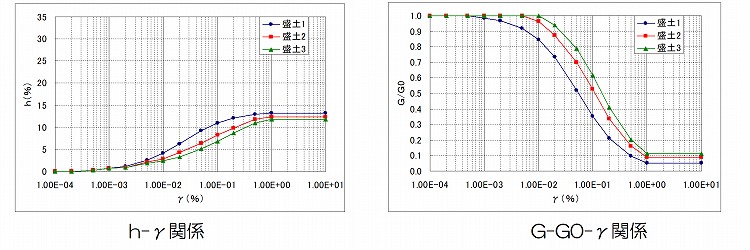
5.地盤の動的変形特性の設定
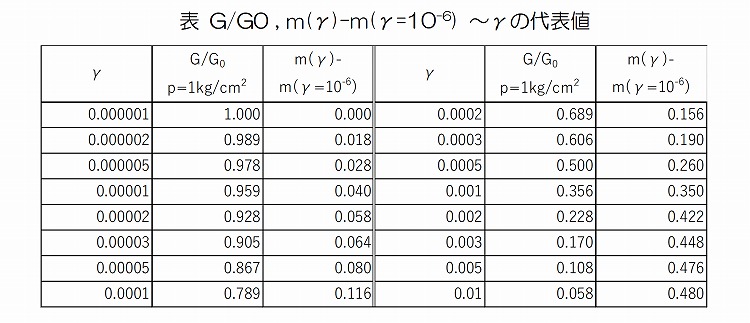
地盤の動的変形特性(G/G0~γおよびh~γ)については、盛土部については「設計要領」に記載されているもののうち、砂質土に最も近いと判断される「マサ土」のひずみ依存特性を用いるものとする。これを拘束圧pごとに「設計要領」にしたがい、土木研究所の拘束圧依存式を反映させて下記の補正を行う。
 土研式の拘束圧依存式を以下に示す。
土研式の拘束圧依存式を以下に示す。
6.ゾーン区分に基づく物性値および境界条件の設定
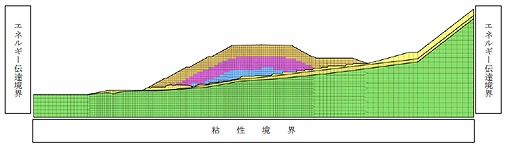
動的解析モデルにおける底面および側面における境界条件を示す。側面はエネルギー伝達境界、底面は粘性境界とした。
地震波形は基盤面(粘性境界)において入力するものとする。
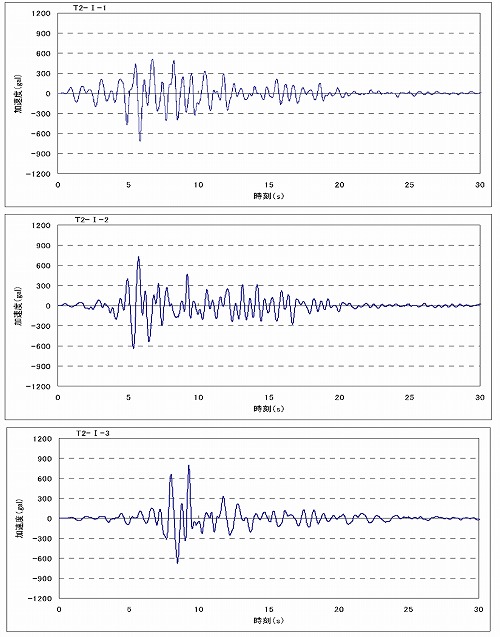
7.入力地震波(基盤入力)の設定
動的解析に用いる設計地震動波形(基盤入力)を下図に示す。地震波形は道路橋示方書に示されているレベル2 タイプⅡ地震動の3 波(T2-Ⅰ-1、T2-Ⅰ-2、T2-Ⅰ-3)とする。
道路橋示方書の波は地表面波であり、本来は基盤面まで引き戻す必要があるがここでは省略し、地表面波を基盤面に入力するものとする。
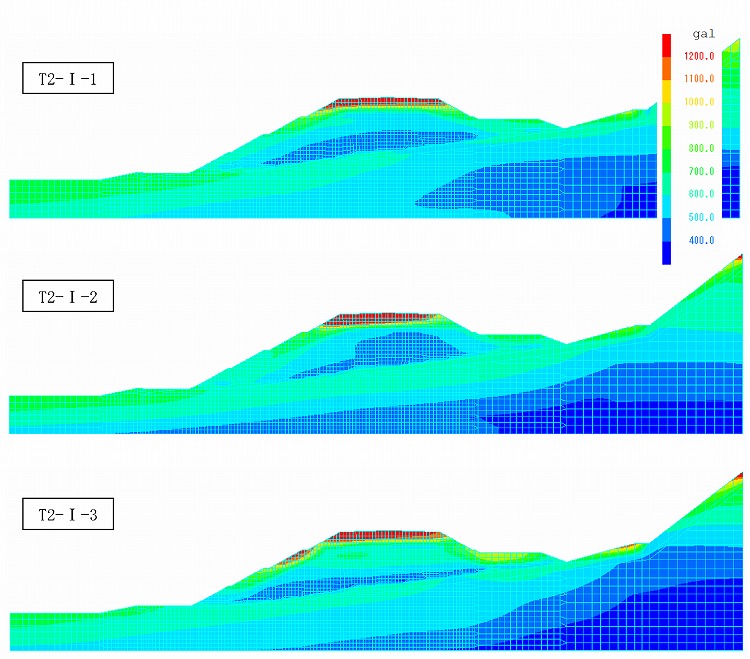
8.等価線形解析
動的解析(等価線形解析)から得られる水平方向最大応答加速度コンター図を示す。いずれの波形に対しても、水平方向最大加速度は盛土天端付近において1200gal 程度の発生が認められる。
9.円弧すべり面の設定および等価加速度の算出
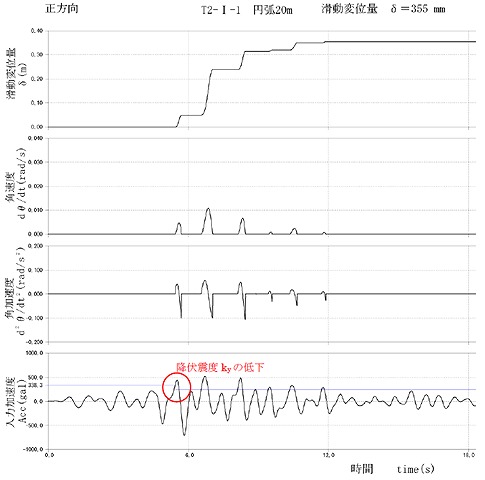
残留変位量を求める3種類の円弧(半径20m、30m、50m)を想定し設定する。
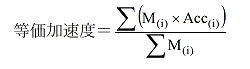
M(i):各節点の質量,Acc(i):各節点の応答加速度波形
10.ニューマーク法による残留変位量の算定
想定したすべり円弧ごとに残留変位量の3波平均を算出し、許容変位量と比較する。
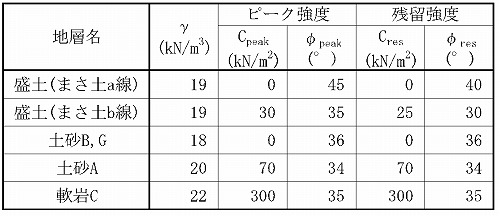
ニューマーク法ではそれぞれのすべり面に対して安全率Fs=1.0となる降伏震度を求める。すべり面の降伏震度を算出する土質定数を下表に示す。ここでピーク強度は円弧のすべり出し時の降伏震度となり、以降の超過震度を求める降伏震度は残留強度により求める。
円弧すべり土塊の運動方程式によって、先に求めた等価加速度の時刻歴のうち降伏震度を超える震度でのすべり土塊の慣性モーメントと地震力による抵抗モーメントと滑動モーメントの比が角加速度となるため、これを積分して角速度とする。ここですべり方向が1方向となるよう角速度が正の区間のみ積分を行う。さらに角速度を積分し回転角θを求める。最後にすべり円弧R×θとして残留変位量を算出することができる。
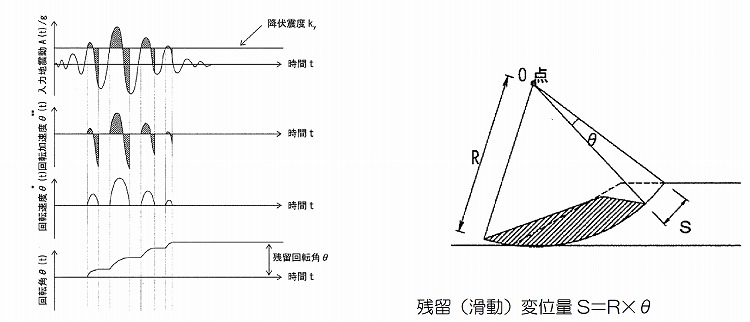
同様に3つの想定円弧、3つの地震波に対する滑動変位量を算出し平均値を下表に示す。
計算の結果、円弧20m、30m、50mの残留変位量はそれぞれ539mm、314mm、512mmとなり、
円弧20mの場合の残留変位量が最大となった。

許容変位量で規定されたものはないが、300~1000mm程度であれば応急処理を行えば車両通行が可能ともされている。実際には個別に総合的な評価を行うものである。
参考文献
3) 道路橋示方書・同解説 Ⅴ耐震設計編,(社)日本道路協会,平成29年3月