1次元と2次元での圧密沈下計算結果比較
解析全般 2017.07.311. はじめに
圧密による沈下量を求めた場合、1次元圧密計算での計算結果と2次元圧密FEMでの計算結果に大きな差違が認められることがあります。そもそも、1次元圧密計算はTerzaghiの圧密理論を用いており、2次元圧密FEMはBiotの圧密理論と関口・太田の弾塑性モデルを用いています。また、解析パラメータとして使用する土質試験結果も異なる部分が多いため、異なる結果になることに疑問は無いのですが、この差違はどのようにして生じているのでしょうか。
ここでは、同じサイトにおける土質試験結果を元にパラメータを設定した

の結果を比較してみました。
2. 1次元圧密計算
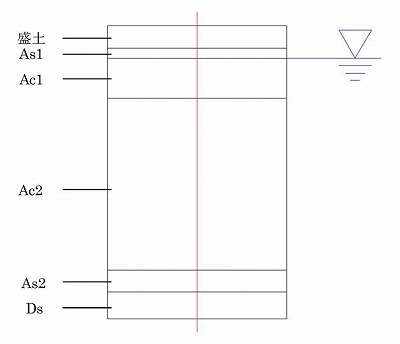
図1に1次元圧密計算のモデル図を示します。このモデルを用いて、盛土を載荷した場合の圧密計算を行いました。砂層は非圧密層とし、粘土層の圧密沈下計算には⊿e法を用いました。
3. 2次元圧密FEM概要
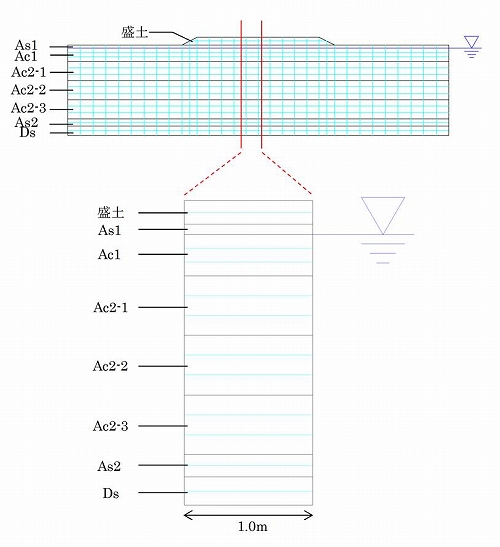
図2に2次元圧密FEMのモデル図を示します。1次元と同じく盛土を載荷した場合の圧密解析を行いました。1次元単柱モデルは、図中の赤線部において要素幅1.0mとしてモデル化しました。
層区分は1次元圧密計算モデルと同じですが、層厚が大きい粘土層は層を3分割してパラメータを設定しました。
4. 解析結果比較
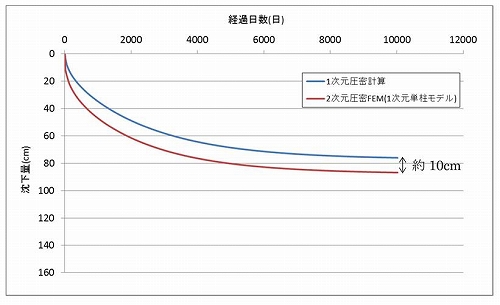
図3に1次元圧密計算と2次元圧密FEM(1次元単柱モデル)の時間-沈下曲線を示します。1次元圧密計算では砂層の沈下量は0cmですが1次元単柱モデルでは砂層の沈下量が7cm程度であることを考慮すると、ほぼ一致していると考えられます。先に述べたように、パラメータに使用している土質試験結果が異なっている割には、沈下量はかなり近い値になっています。
使用パラメータはまったく同じですので、この差が生じる原因は、1次元と2次元のモデルの違いであることがわかります。
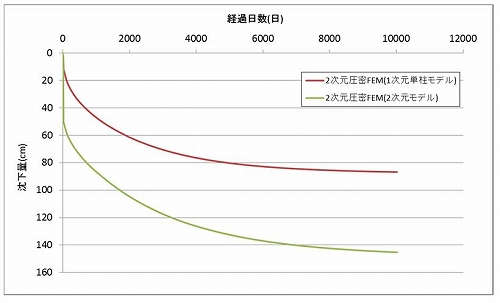
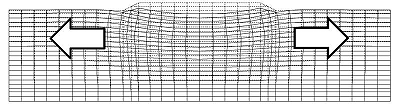
図5に2次元モデルの変形図を示します。この図を見ると盛土下周辺の地盤が大きく水平方向に変形しており、この影響で盛土部が大きく沈下していることがわかります。
1次元モデルでは、この水平方向の変形は生じません。したがって、2次元モデルと1次元モデルの沈下量の差はこの水平変位によることがわかります。
これは、1次元圧密計算でも同じです。
5. まとめ
以上より、1次元と2次元では水平方向の変形の有無により沈下量に大きな違いが生じることがわかりました。なお、今回の検討では1次元圧密計算と2次元圧密FEM(1次元単柱モデル)の結果は近い値となりましたが、そもそも使用する物性値が異なるので、この両者の比較においても結果が大きく異なることは起こり得ると思われます。ご注意ください。