1. はじめに
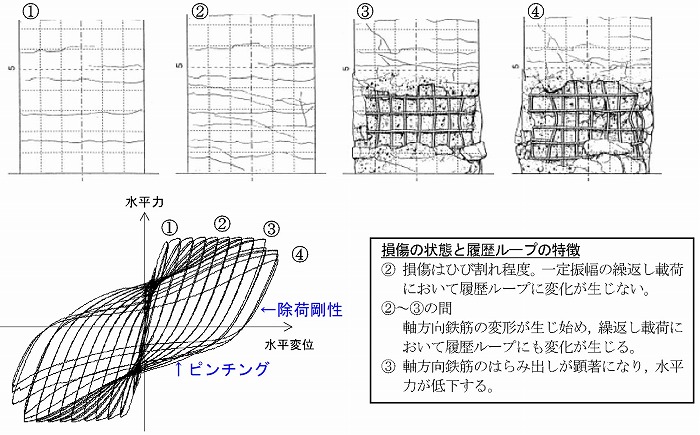
　鉄筋コンクリート橋脚の曲げ破壊型の損傷過程は図-1となります．実験での履歴形状が紡錘型であれば再現解析の難易度は比較的低いのですが，塑性変形が大きくなり，逆S字型あるいはスリップ型に移行すると，除荷剛性やピンチングを高精度で再現することは容易ではありません．今回は，DIANAにおいて軸方向鉄筋の座屈を考慮できる構成則を使用することで，ＲＣ橋脚の正負交番載荷実験に対しての再現性向上を試みた事例を紹介します．

図-1　曲げ破壊タイプの鉄筋コンクリート橋脚の水平力-水平変位関係と損傷の進展¹⁾

2. 計算対象
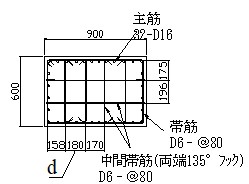
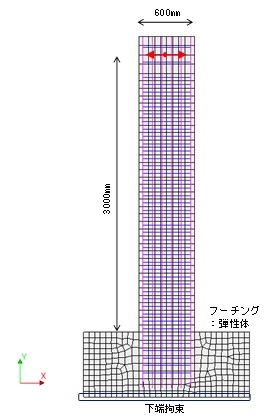
　矩形断面のRC脚の交番載荷実験²⁾を計算対象モデルとしました． 試験体諸元および配筋図を表-1および図-2に示します．実物に対し縮尺1/5を想定した諸元を有する矩形断面900×600㎜とし，主鉄筋比は1.18％，横拘束筋比は0.88％としています．軸方向鉄筋の芯かぶりを40㎜としています．

表-1　試験体諸元²⁾

図-2　試験体柱断面配筋図（単位：㎜）²⁾

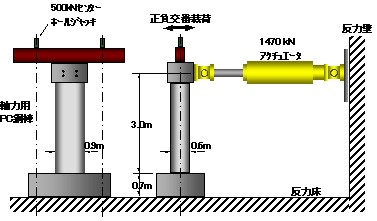
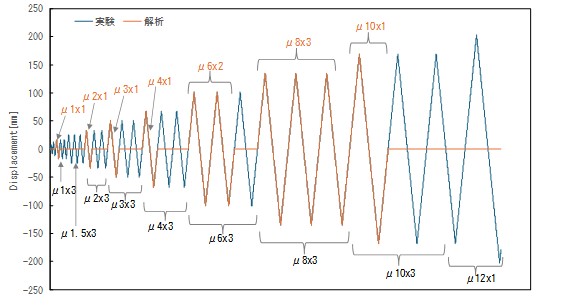
　載荷装置を図-3に示します．試験体はPC鋼棒によってフーチング部を反力床に固定し，試験体頂部に取り付けた1470kNアクチュエータによって正負交番載荷しました．軸力は，上部構造荷重と橋脚自重によって実橋脚基部断面に生じる軸圧縮応力度を想定し，一定軸力（0.8MPa）をPC鋼棒によって作用させています．水平力は，荷重制御によって加力し，続いて変位制御により塑性率μ=1.0,1.5,2.0・・・をそれぞれ3サイクルずつ繰り返しています．

図-3加力装置²⁾

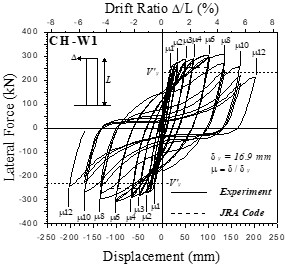
　試験体基部の最終破壊状況を図-4に，荷重変位関係を図-5に示します．曲げひび割れは，水平力P=80kNで試験体基部に発生しました．降伏変位はδy=16.9㎜であり，最外縁の主筋が降伏ひずみを越えたのは，μ=1.0～1.5です．柱基部より約1.0D（D:柱せい）における曲げひび割れは，μ=1.5(P=265kN)において曲げせん断ひび割れへと移行しました．μ=6.0～8.0において最大耐力（P＝307kN）を示し，柱基部に圧壊が生じました．μ＝8.0の繰り返し載荷において，かぶりコンクリートの剥落に伴い，中間帯鉄筋が抜け出し，主筋座屈および破断による耐力低下が生じました．

図-4最終破壊状況²⁾

図-5水平力-水平変位関係²⁾

3. 解析条件
　図-6にモデル図を示します．平面応力要素を使用した2次元モデルとし，鉛直方向の要素分割は帯鉄筋間隔80mmを基本としました．

図-6計算モデル図

　材料物性値は前述の表-1を踏襲し，使用した構成則および計算条件を表-2に示します．コンクリート標準示方書に準拠した構成則を使用し，座屈長は土木研究所資料³⁾に準じて算出しました．フーチング定着部の処理，かぶりコンクリートとコアコンクリートの物性値の使い分け，圧縮軟化パラメータ設定等，様々な工夫を行っていますが詳細は割愛します．気になった方はホームページの問い合わせフォームでアクセスいただければと思います．

表-2使用モデルおよび計算条件

　荷重は実験と同じ軸力を与えた後，図-7に示す繰り返し水平変位載荷としました．計算時間の短縮のため，図-5の水平力-水平変位関係で繰り返し載荷の影響が小さいと考えられるμ=4.0までは1サイクルずつの載荷とし，μ=6.0は2サイクル載荷，μ＝8.0は3サイクル載荷としました．実験ではμ=10.0で軸方向鉄筋が破断したことから，μ=10.0の1サイクル終了を最終荷重ステップとしました．

図-7載荷ステップ

4. 計算結果
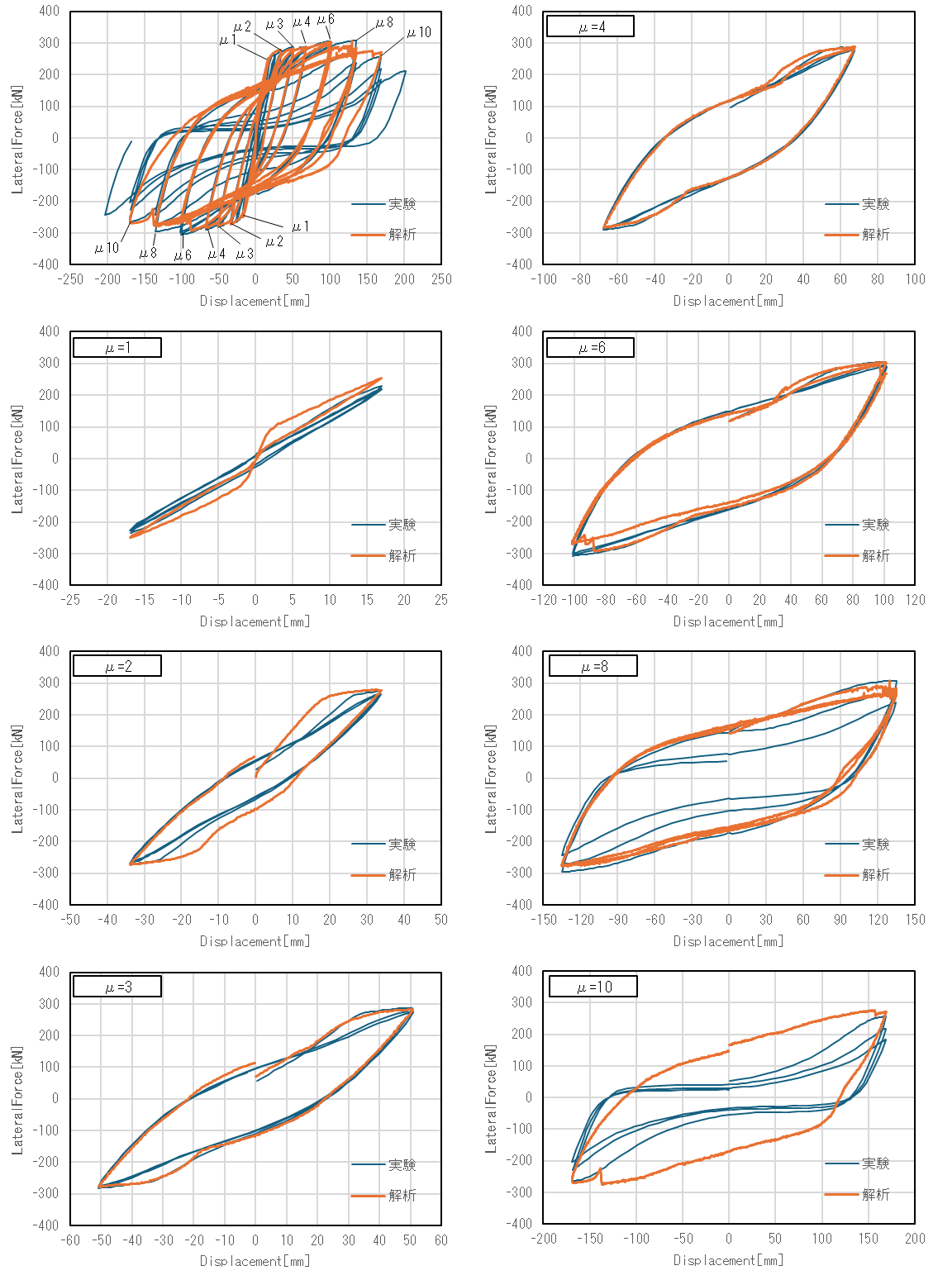
　図-8に水平荷重-水平変位関係を示します．μ=6.0までは再現性が高い結果が得られています．μ=8.0の1サイクル目までは良好な再現性が確認できますが，2サイクル目以降，実験のような繰り返し載荷に伴った履歴ループの絞り，すなわちピンチング挙動が再現できていません．これは使用構成則が鉄筋破断のような大変形まで模擬できないことが理由と考えられます．但し，μ=8.0からμ=10.0で座屈による耐力低下は再現できています．

図-8水平力-水平変位関係（実験および解析）

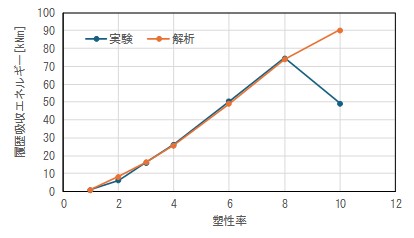
　図-9に履歴吸収エネルギー（1サイクル目のみ）を示します．前述の通り，μ=10.0ではピンチングの再現性が不十分であることから実験結果のような顕著なエネルギー低下が得られませんでした．

図-9履歴吸収エネルギー（実験および解析）

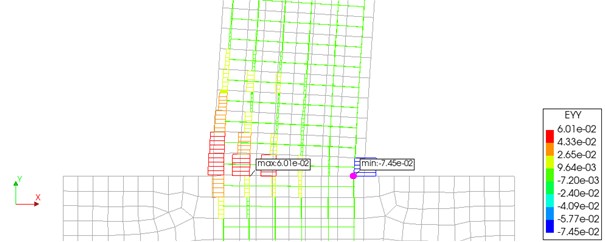
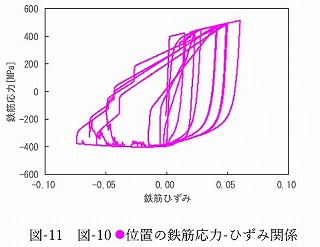
　図-10にμ=10.0での鉄筋ひずみ分布図を示します．圧縮側の最外縁鉄筋下端に座屈によるひずみが集中していることがわかります．図-11に当該位置の鉄筋応力-ひずみ関係を示します．圧縮域でクチバシ型を呈す座屈モデルの履歴形状が確認できます．

図-10鉄筋ひずみ図【μ＝10.0（→方向載荷時）】

5. まとめ
　DIANAによるRC橋脚の正負交番載荷実験の再現解析事例を紹介しました．現状の鉄筋構成則では破断は模擬できないものの鉄筋座屈による耐力低下を再現可能でポストピーク挙動の把握に有効な数値シミュレーションの実施が可能となりました．