本コラムでは鉄筋コンクリート柱の曲げモーメント－曲率関係(以下M-φ関係と記述)の算出に関して、鉄道標準と道路橋示方書による比較を行います。

１．はじめに
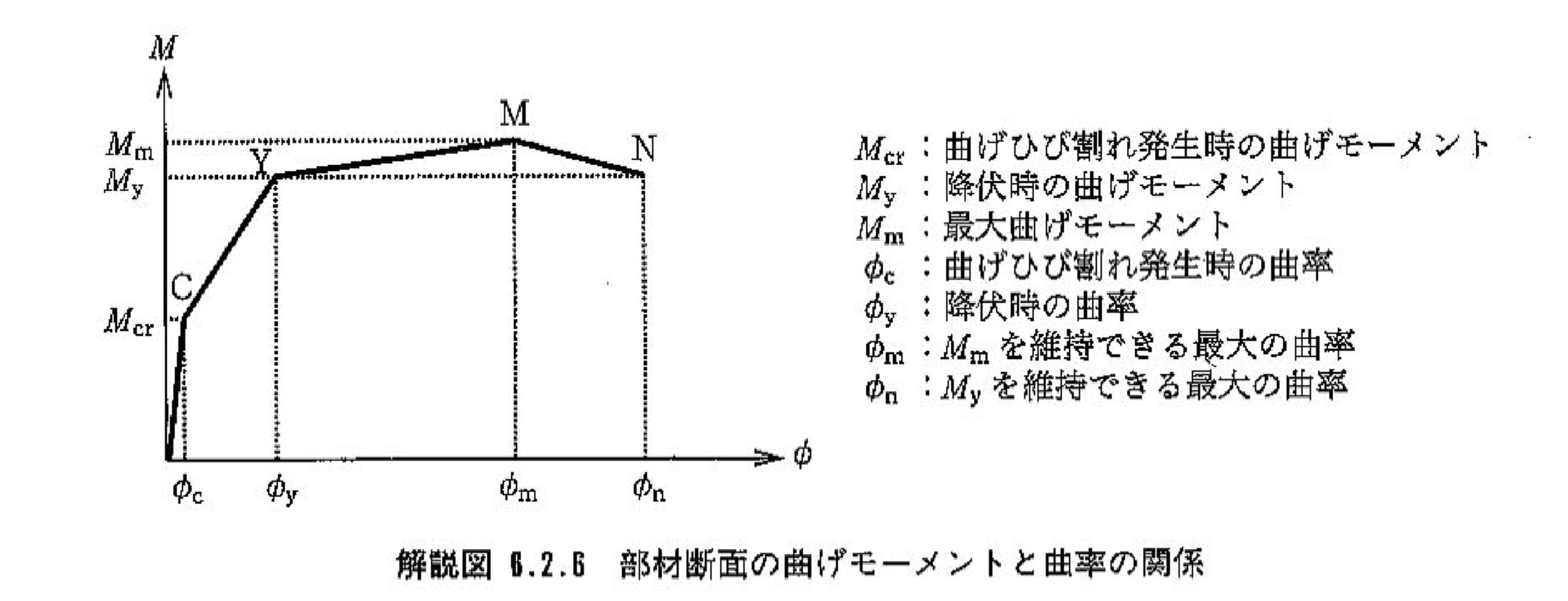
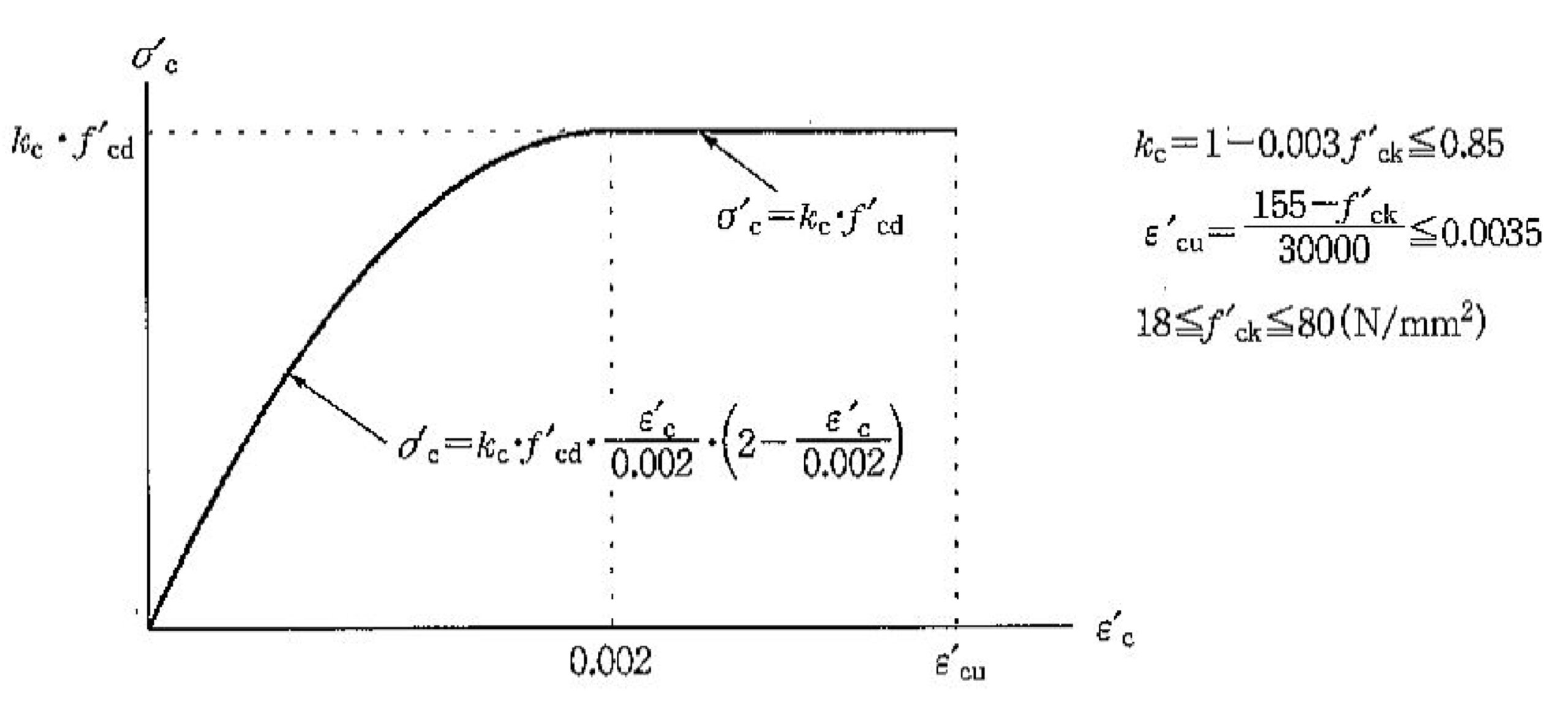
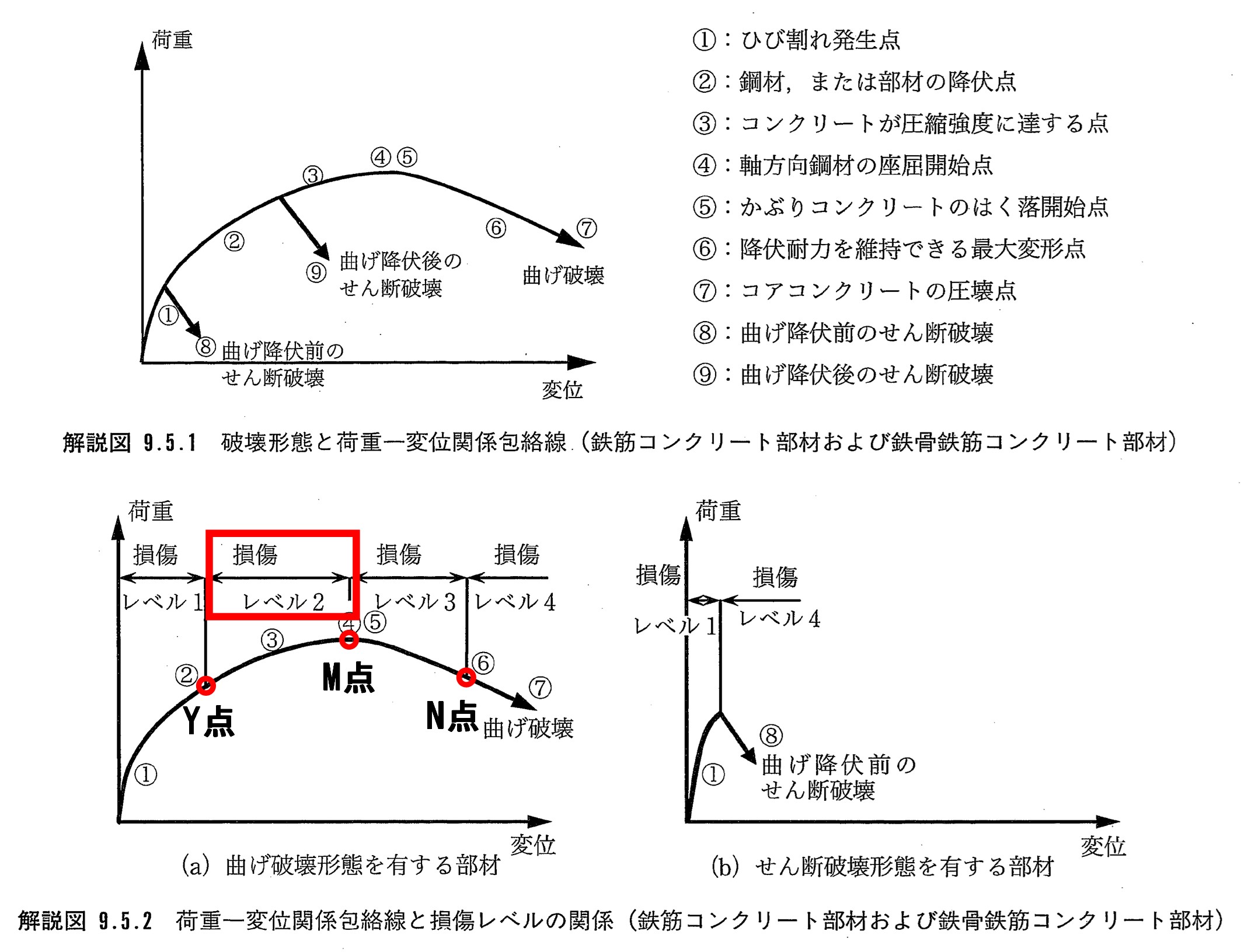
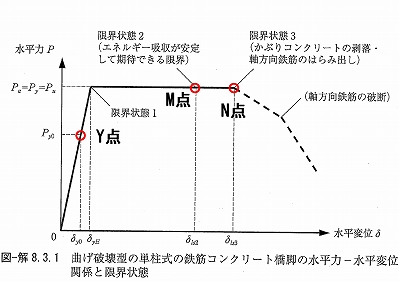
　鉄道構造物等設計標準・同解説では図1に示すC点、Y点（初降伏）、M点、N点で構成されるM-φ関係のうちM点を下記のとおり定義しています。最大曲げモーメントM_mは“コンクリートの圧縮ひずみが図2に示す終局ひずみε’_cuに達するとき”、曲率φ_mは“式1より算出したθ_pmを等価塑性ヒンジ長L_pで除した値”と定義しています。
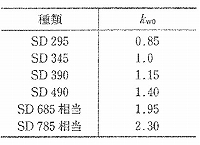
　ここで、曲率φ_mはθ_pmを算出する式-1において帯鉄筋強度を考慮する係数k_w0と帯鉄筋比p_wを組み込むことで帯鉄筋の拘束効果による変形性能への影響を評価していることが分かります。

図1　曲げモーメント-曲率関係

図2　コンクリートのモデル化された応力-ひずみ曲線

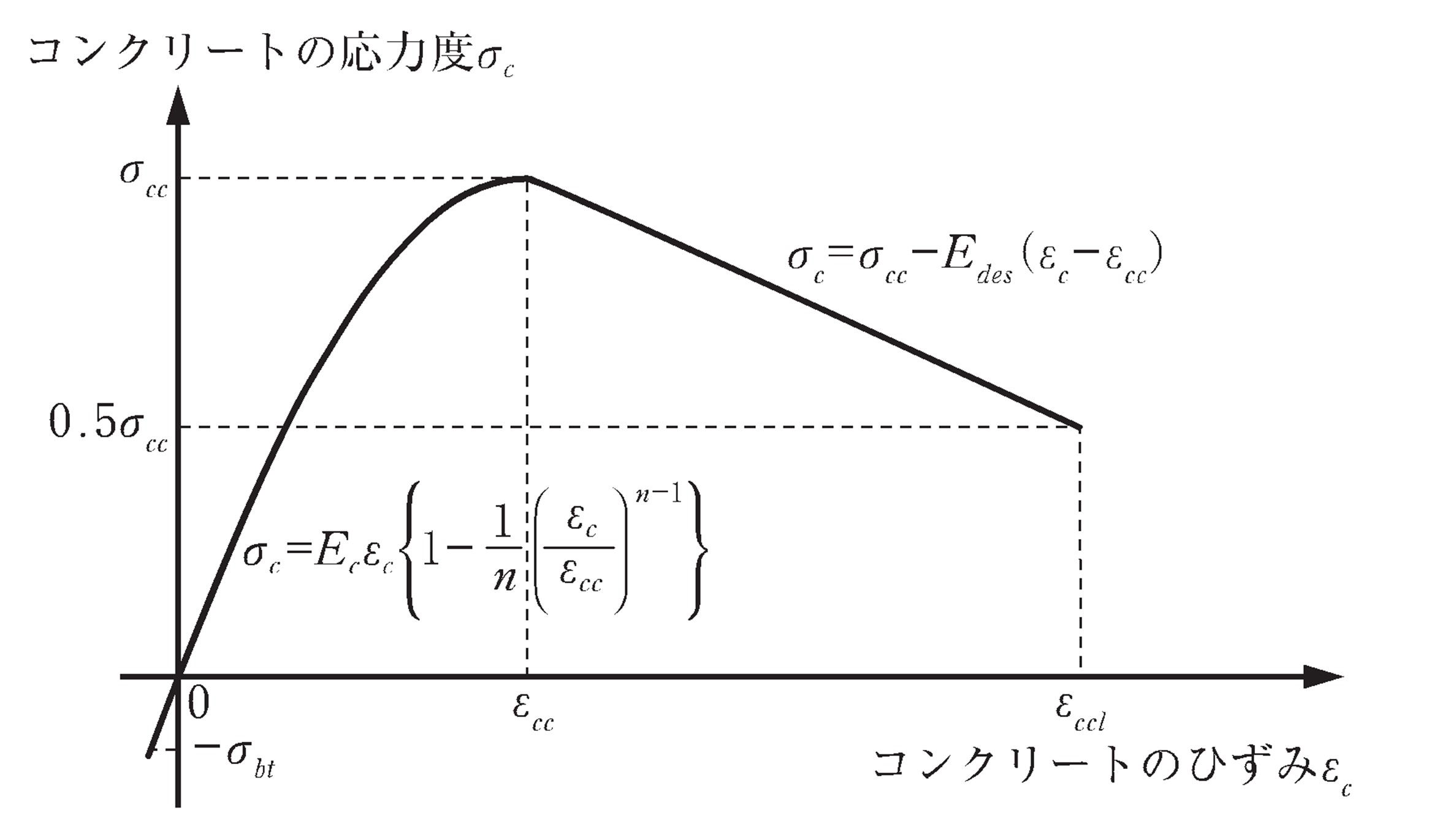
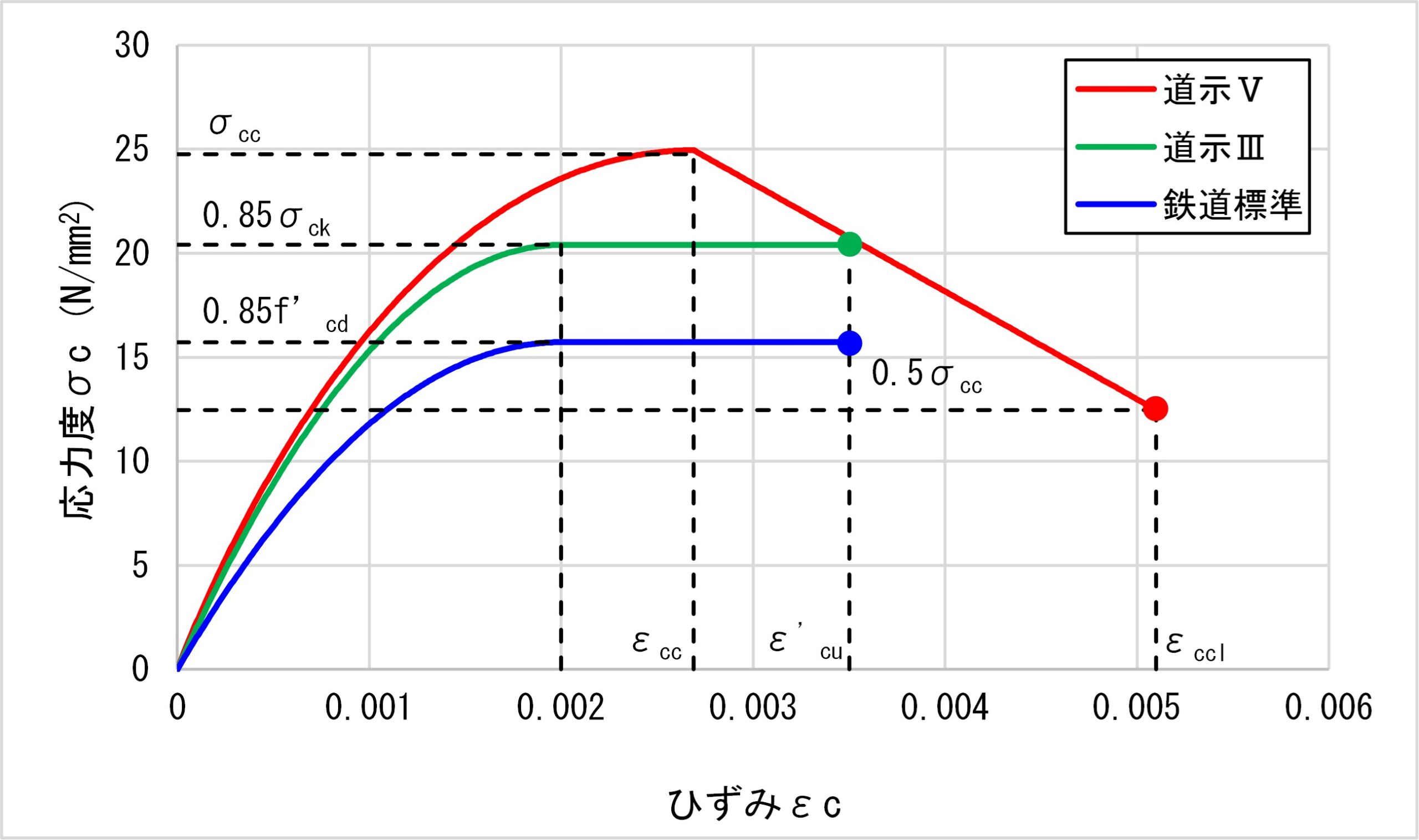
　一方、道路橋示方書・同解説Ⅴ耐震設計編H29（以下、道示Ⅴと記述）では、コンクリートの応力-ひずみ曲線は図3に示すとおりです。コンクリートの最大圧縮応力度σ_cc（式2）、ひずみε_cc（式3）、降下勾配E_des（式4）を横拘束鉄筋の体積比ρ_s（式5）、横拘束鉄筋の降伏応力度σ_sy、コンクリートの設計基準強度σ_ckの関数として与えることで、帯鉄筋の拘束効果による変形性能への影響を見込んでいます。

図3　コンクリートの応力-ひずみ曲線（道示Ⅴ）

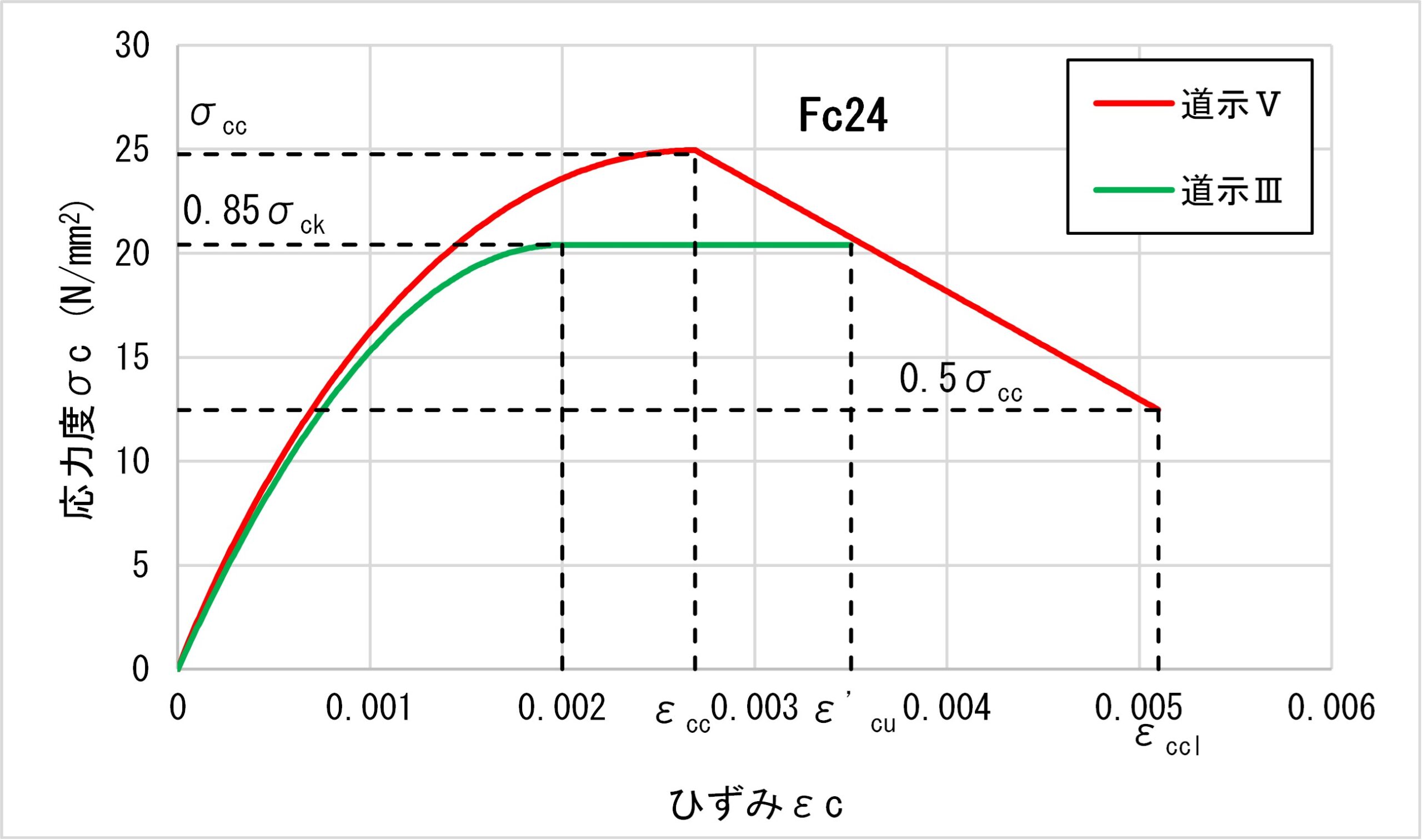
　なお、帯鉄筋の拘束効果による変形性能への影響を見込んでいない道路橋示方書・同解説Ⅲコンクリート橋編H29（以下、道示Ⅲと記述）と道示Ⅴの応力-ひずみ曲線を比較すると図4のとおりで、帯鉄筋の拘束効果によって、コンクリートの圧縮応力と圧縮ひずみが増加していることが分かります。

図4　コンクリートの応力-ひずみ曲線比較

　ここで、対象構造物を既設の標準的なRC鉄道高架橋として耐震性能照査を行うことを想定すると、鉄道標準では要求性能として復旧性と安全性が求められ、表2に示すとおり復旧性では橋脚躯体の損傷レベルは2（もしくは3）となります。図5に示すとおり、損傷レベル2の限界点をM点としています。
　この対象構造物の要求性能である復旧性を道示Ⅴに当てはめると耐荷性能2にあたり、耐荷性能2を満足する橋に求める状態は、限界状態2を超えないことです。従って、本コラムでは鉄道標準におけるM-φ関係のM点を道示Ⅴにおける限界状態2とみなし（図6）、これらを比較します。

図5　荷重-変位関係（鉄道標準）

図6　荷重-変位関係（道示Ⅴ）

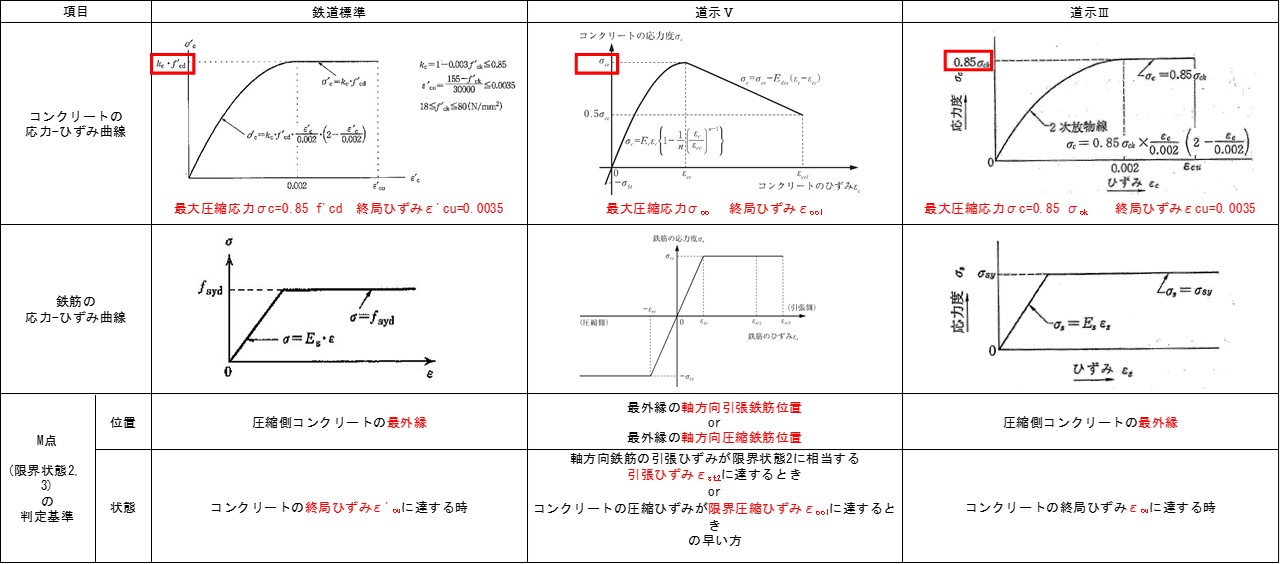
　表3に各基準におけるコンクリートおよび軸方向鉄筋の応力-ひずみ曲線、M点（あるいは限界状態2）に達する時の判定基準に着目し、相違点を示します。なお、帯筋の拘束効果を見込んでいない道示Ⅲの限界状態3も併せて比較します。

　今回は、各基準のM点（限界状態2,3）に焦点を当て、以下に示す①～⑤の比較を行います。

　①鉄道標準における帯鉄筋の有無（無：帯鉄筋比0％）によるM-φ関係の比較（拘束効果の影響）
　②鉄道標準、③道示Ⅴ、④道示Ⅲより算出したM-φ関係の比較
　⑤各基準のM点の比較

　また、M-φ関係は軸力の影響を大きく受けるため、軸力の違いも加味したものとし、各基準における帯鉄筋の拘束効果による曲げ耐力や変形性能への影響を確認します。なお、ここでは軸方向鉄筋の伸び出しは考慮していません。

２．対象構造物
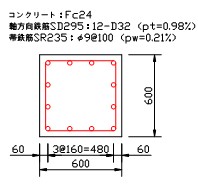
　今回の対象構造物は既設の標準的なRC鉄道高架橋とし、図7に示す高架橋柱基部のM-φ関係を算出します。図8に断面の諸条件を示します。

図7　標準的なRC鉄道高架橋

　　　断面：断面600mm×600mm
　　　　　　軸方向鉄筋SD295-12-D32
　　　　　　帯鉄筋SR235-φ9＠100mm
　　軸応力：1MPa～3MPa
　　※以降、便宜上軸応力を軸力と表記します。

図8　柱基部の断面

３．M-φ関係算出結果比較
　以下に①～⑤の算出結果を示します。

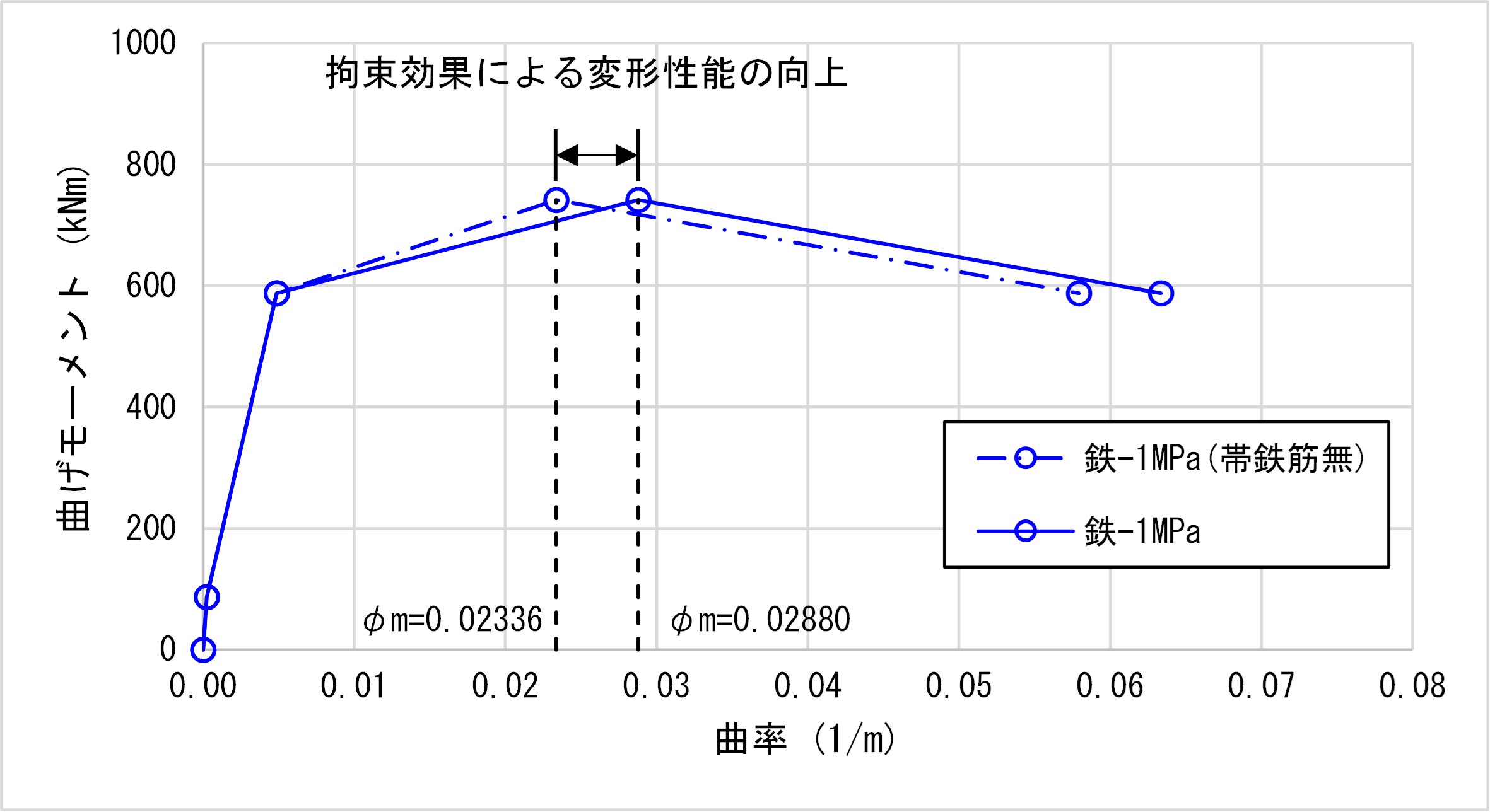
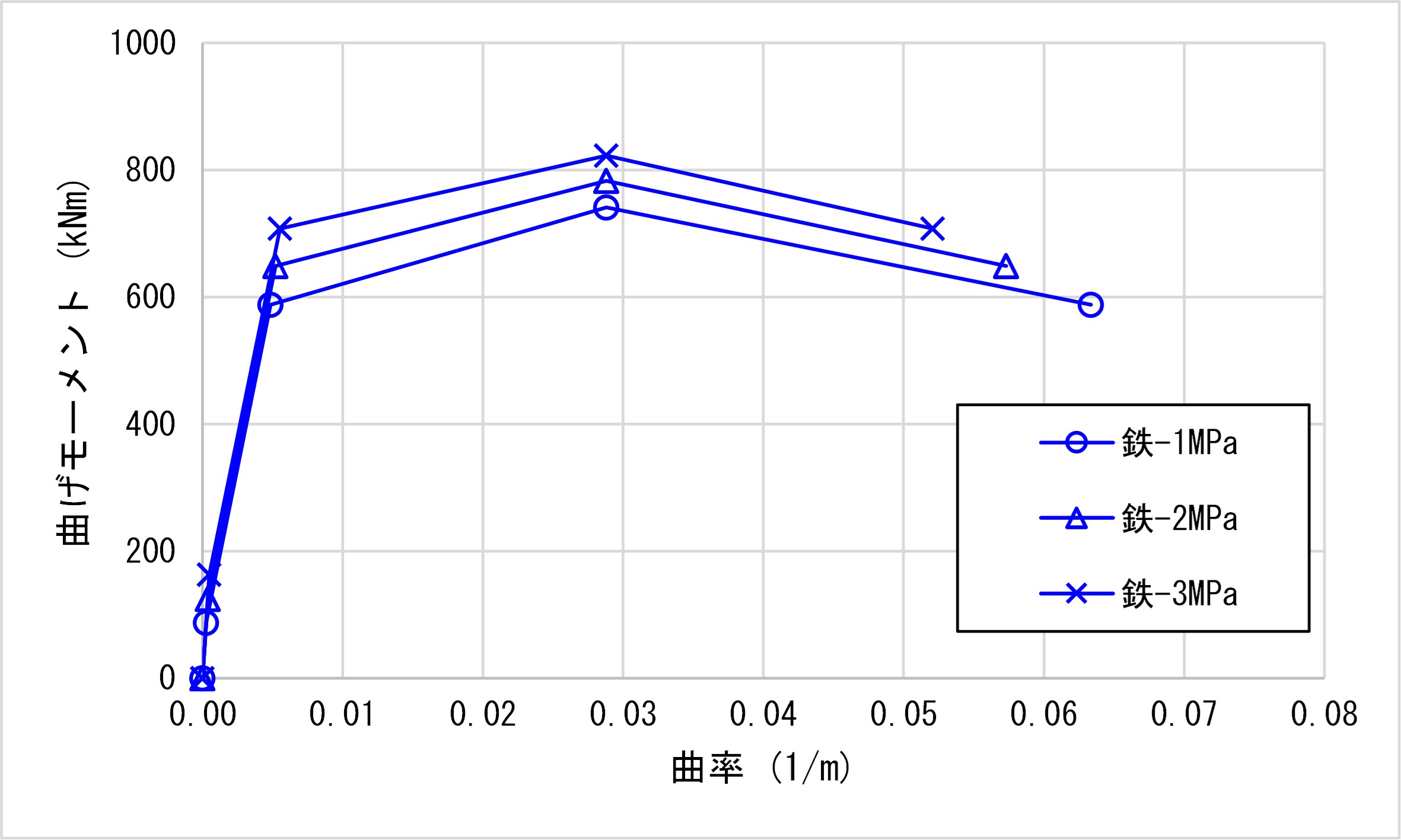
　①鉄道標準における帯鉄筋の有無（無：帯鉄筋比0％）によるM-φ関係の比較（拘束効果の影響）

図9　M-φ関係算出結果（帯鉄筋の有無）

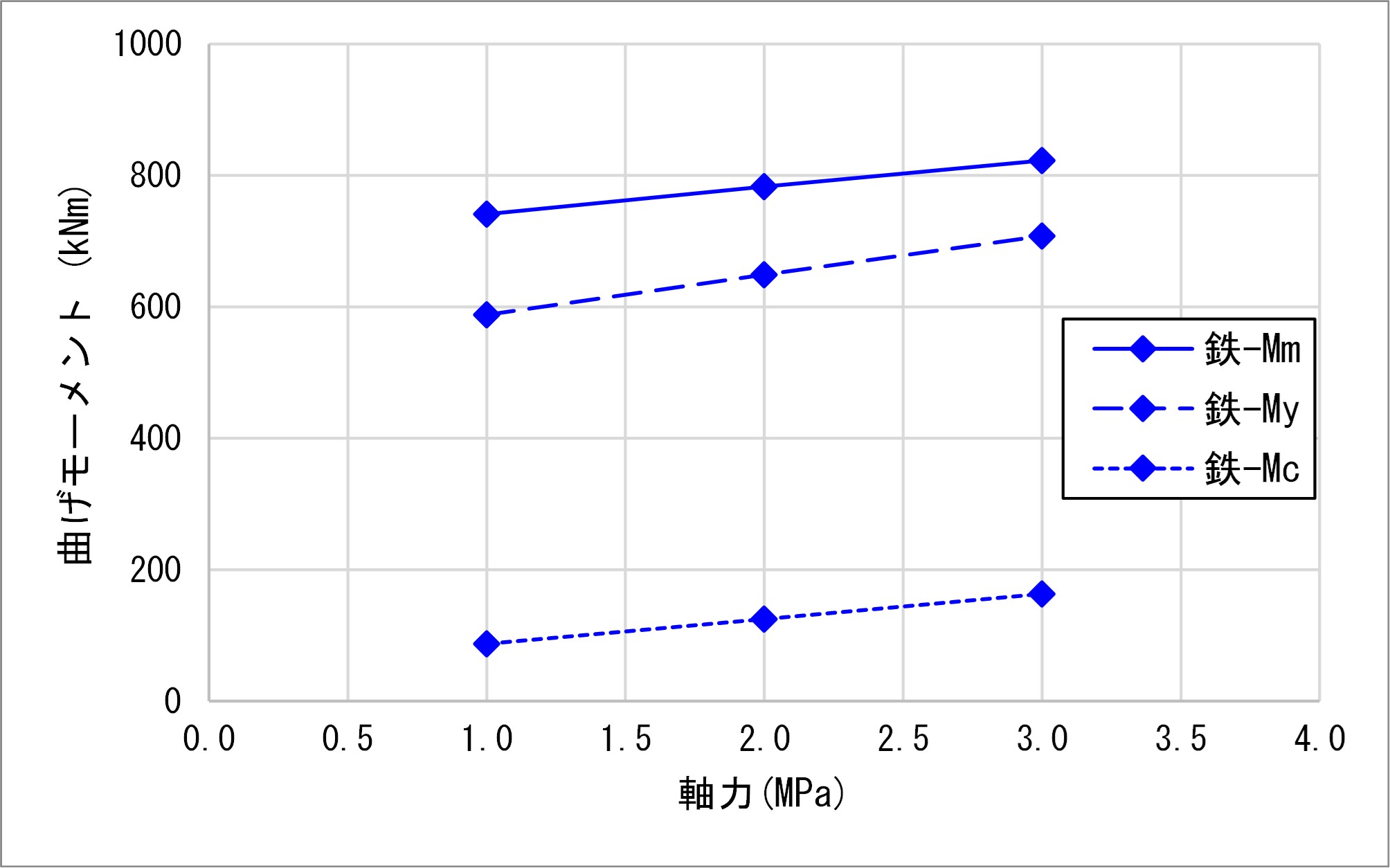
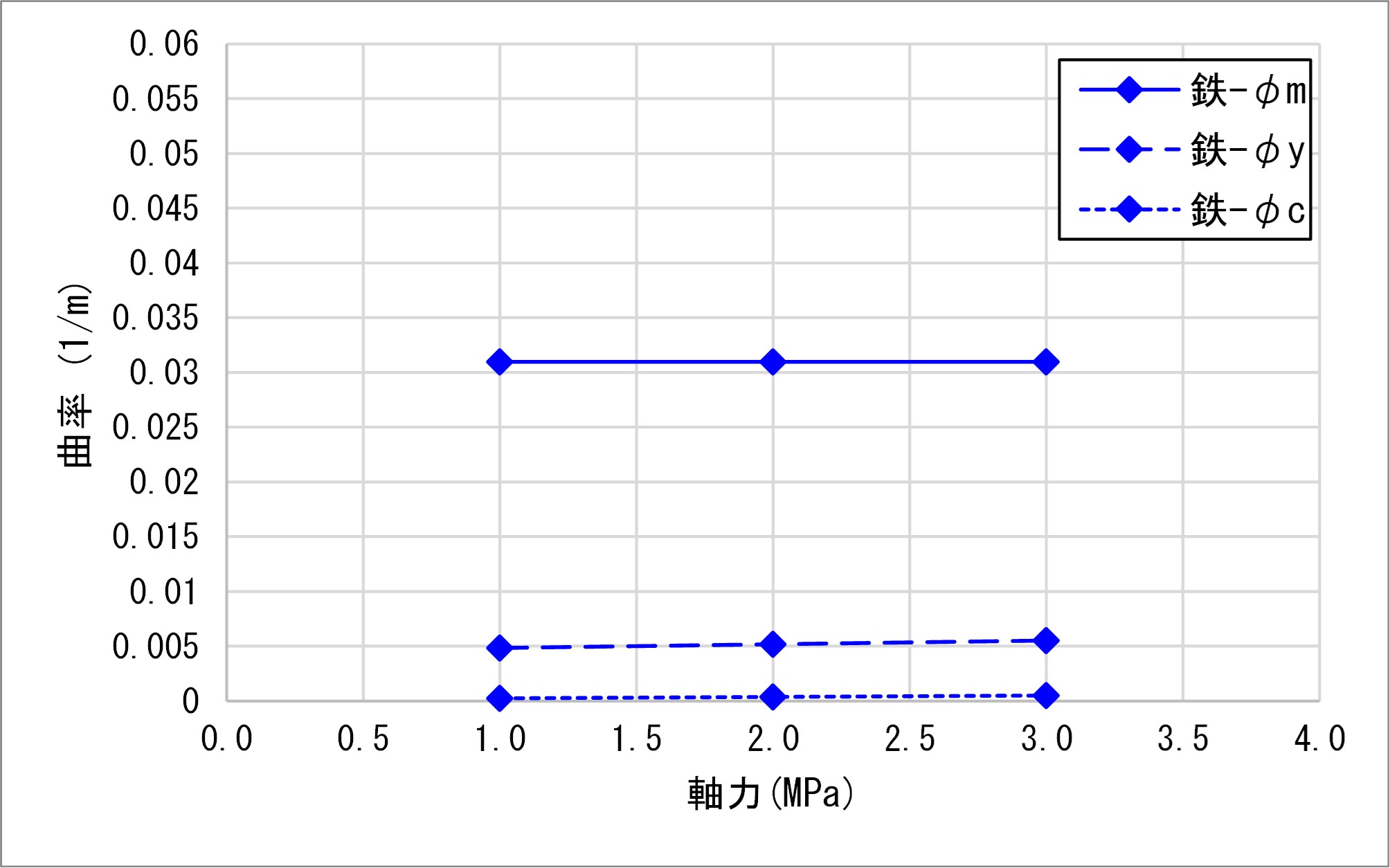
　②鉄道標準によるM-φ関係比較

図10　M-φ骨格曲線（鉄道標準）

図11　曲げモーメントと軸力の関係（鉄道標準）

図12　曲率と軸力の関係（鉄道標準）

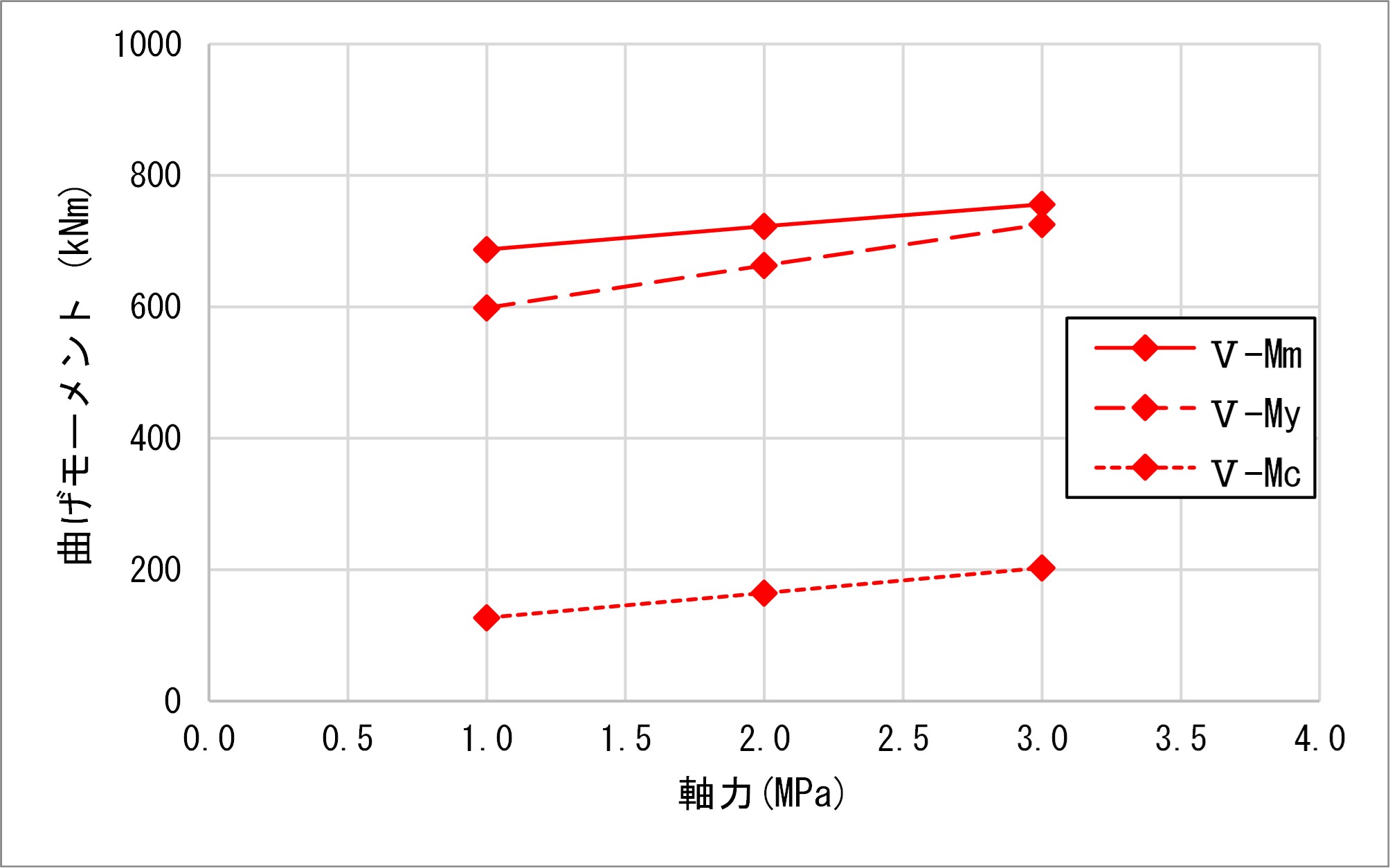
③道示ⅤによるM-φ関係比較

図13　M-φ関係算出結果（道示Ⅴ）

図14　曲げモーメントと軸力の関係（道示Ⅴ）

図15　曲率と軸力の関係（道示Ⅴ）

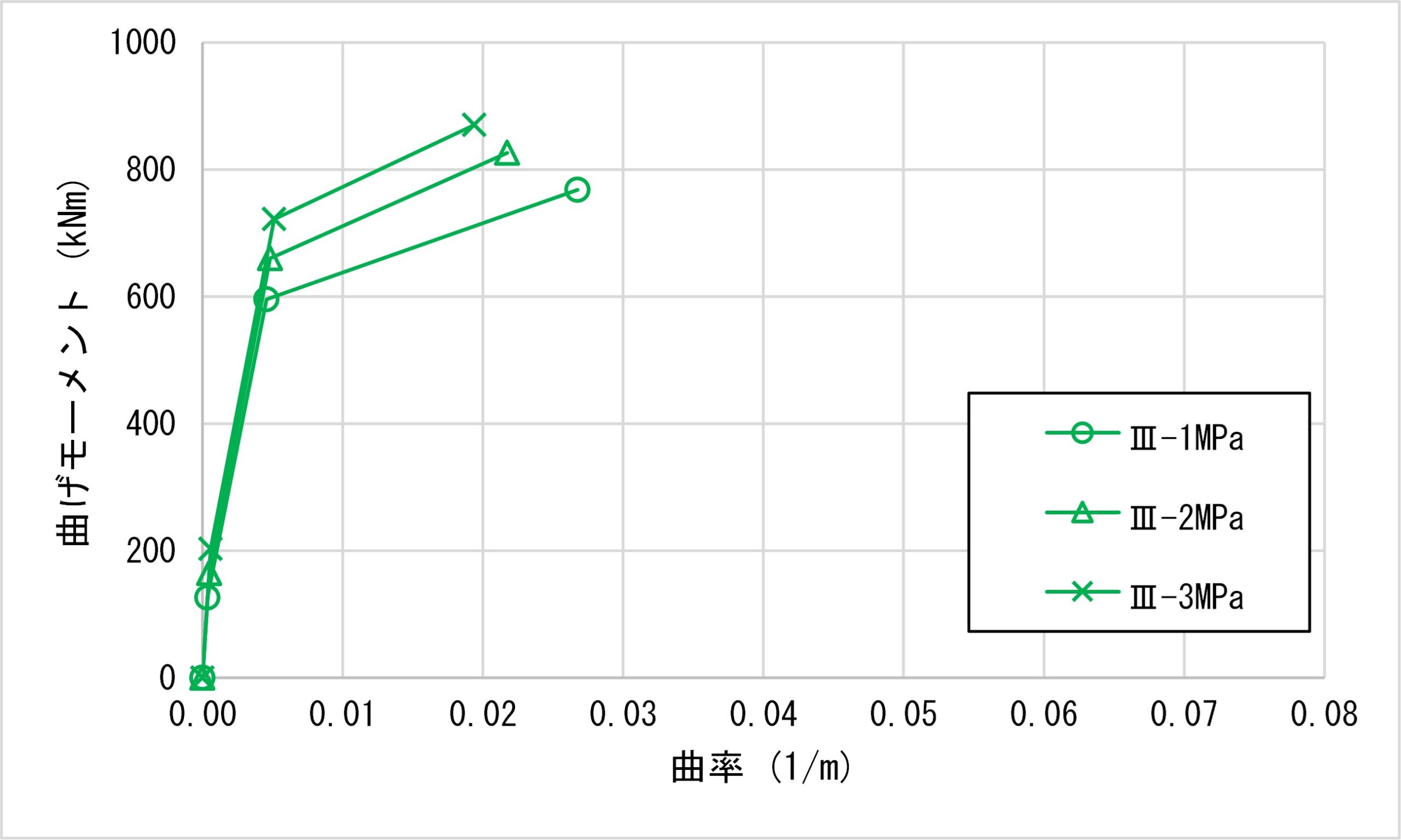
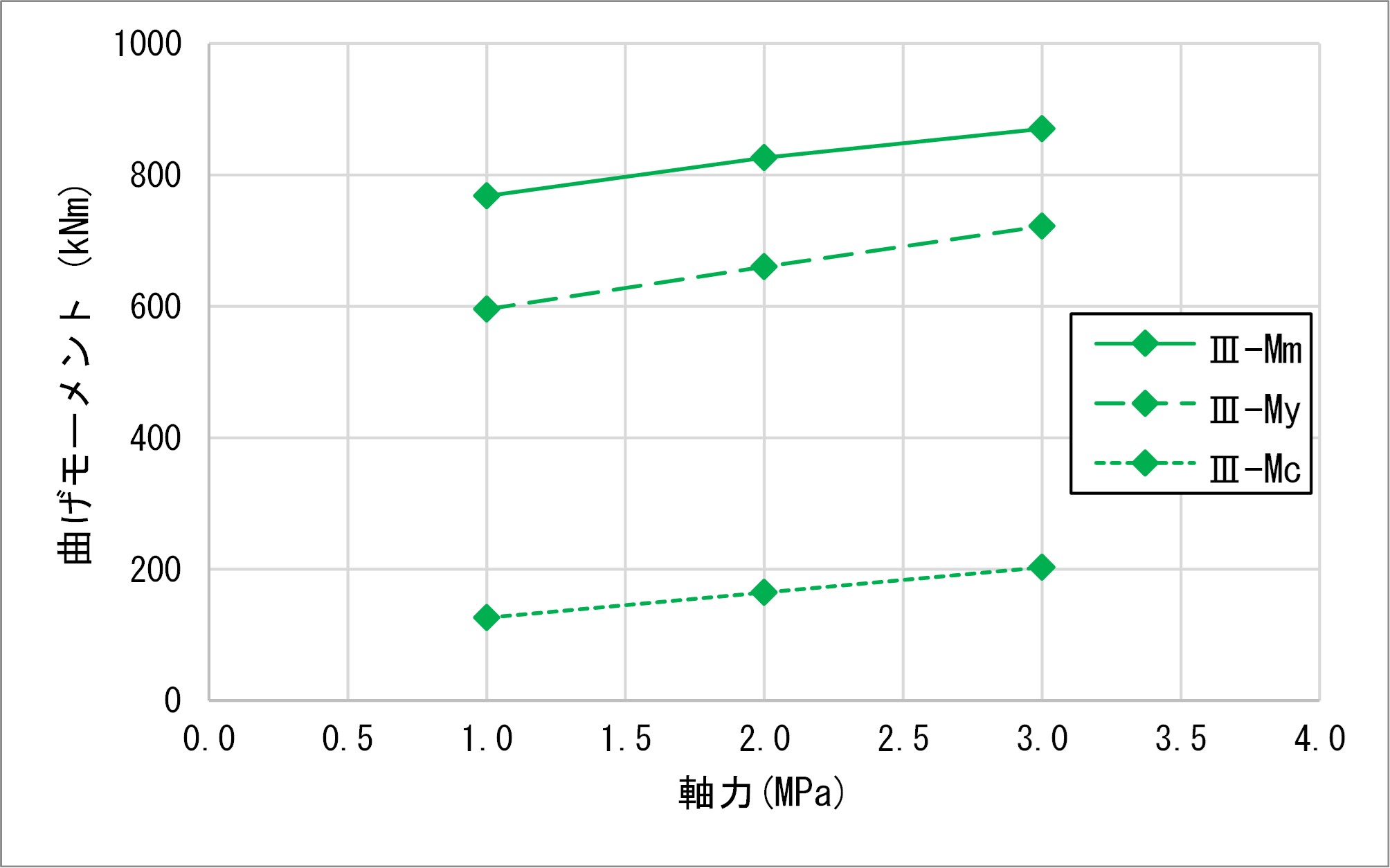
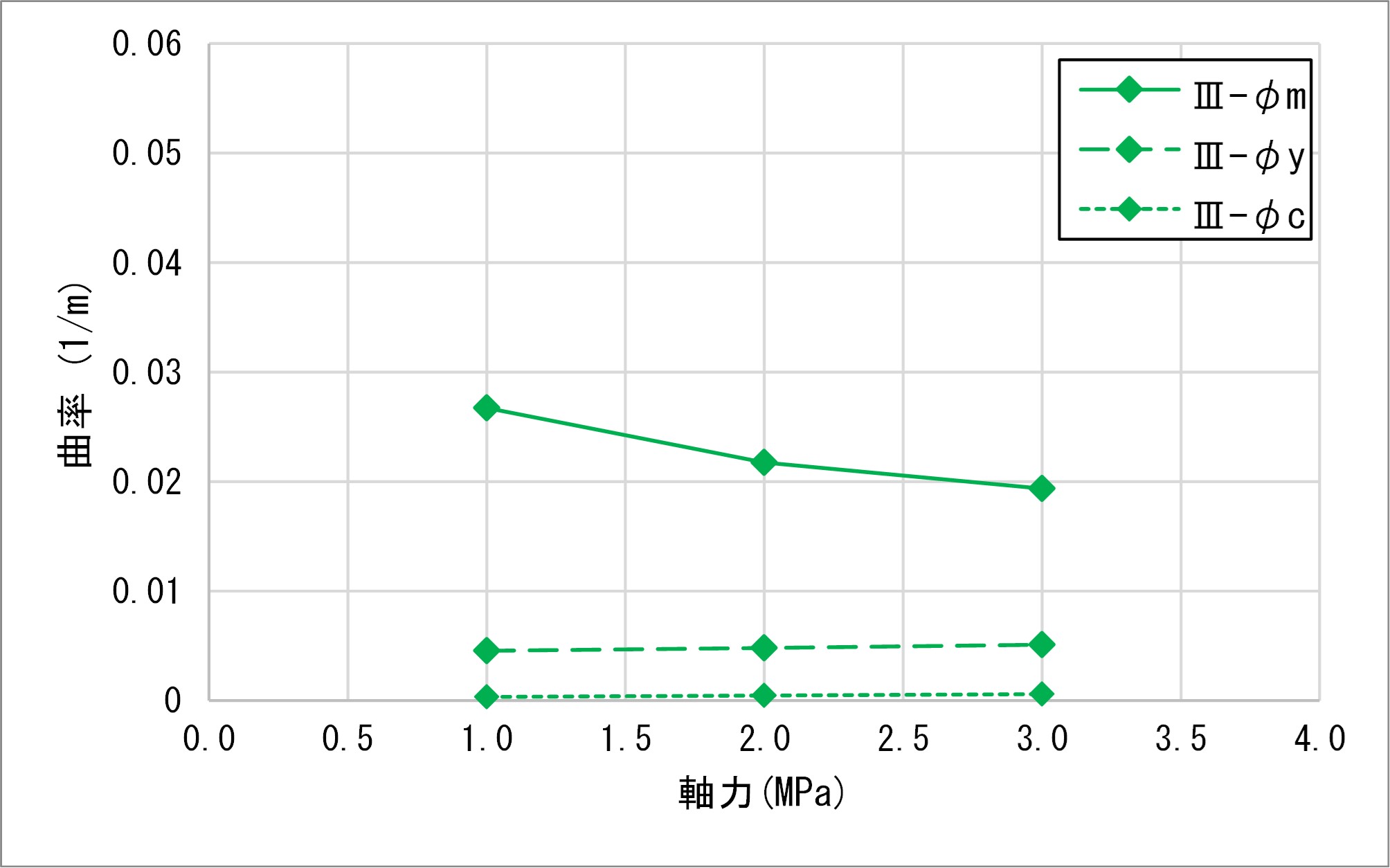
④道示ⅢによるM-φ関係比較

図16　M-φ関係算出結果（道示Ⅲ）

図17　曲げモーメントと軸力の関係（道示Ⅲ）

図18　曲率と軸力の関係（道示Ⅲ）

⑤各基準によるM-φ関係比較

図19　曲げモーメントMmと軸力の関係

図20　曲率φmと軸力の関係

図21　鉄道標準と道路橋示方書によるコンクリートの応力-ひずみ曲線比較

４．まとめ
　今回、鉄道標準および道路橋示方書と軸力によるM-φ関係を比較して分かったことを以下に示します。

1）帯鉄筋の有無による変形性能への影響
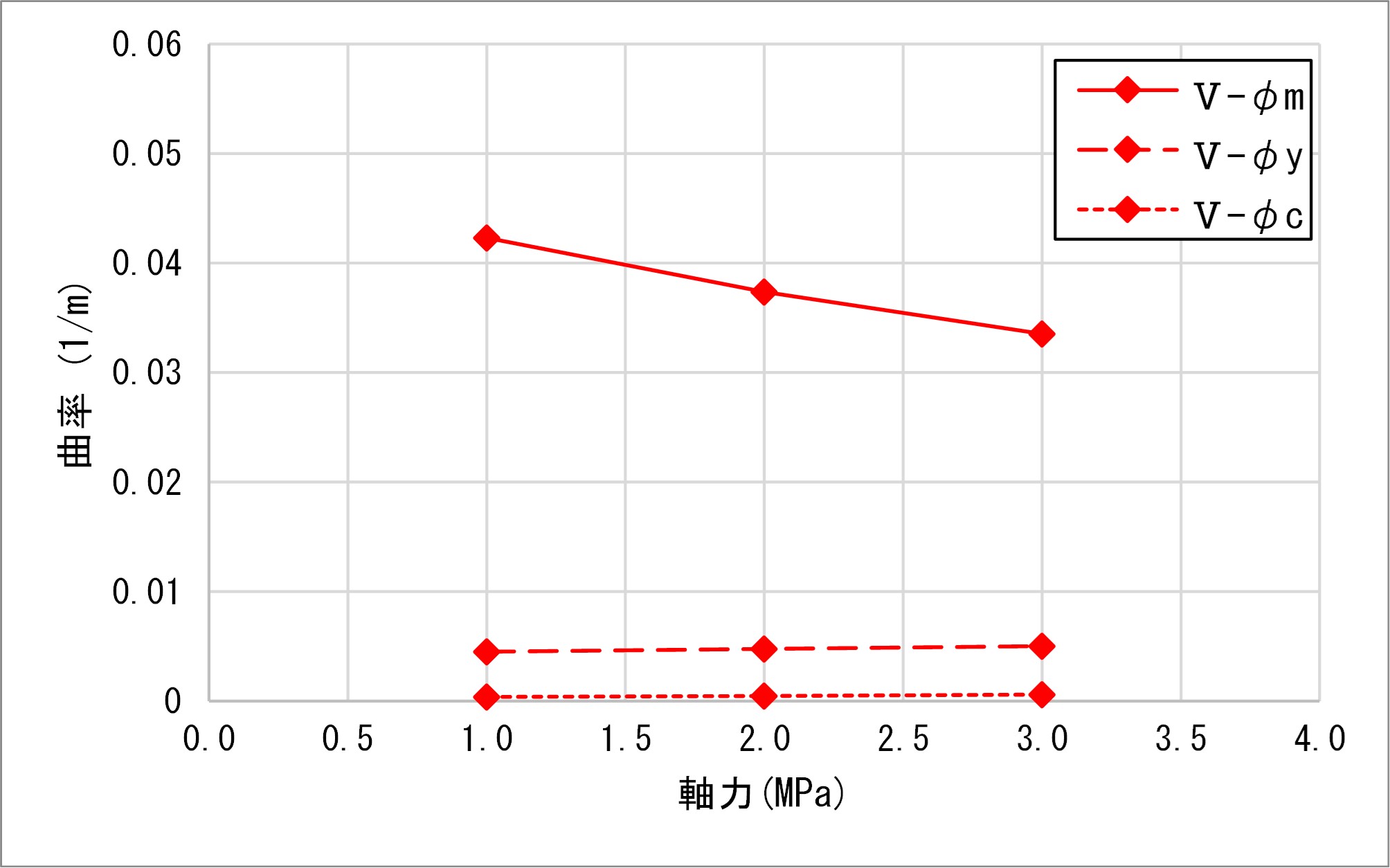
　鉄道標準では、帯鉄筋の拘束による変形性能の向上について、θ_pmで帯鉄筋比p_wのパラメータによって拘束効果が見込まれており、M点の曲率について、明らかに帯鉄筋の影響と思われる計算結果が得られました。この結果より、鉄道標準から得られる曲率で損傷評価を実施する場合は、帯鉄筋の拘束効果を考慮したφ_mとすることで合理的な損傷度評価が可能となります。

2）各基準と軸力による影響
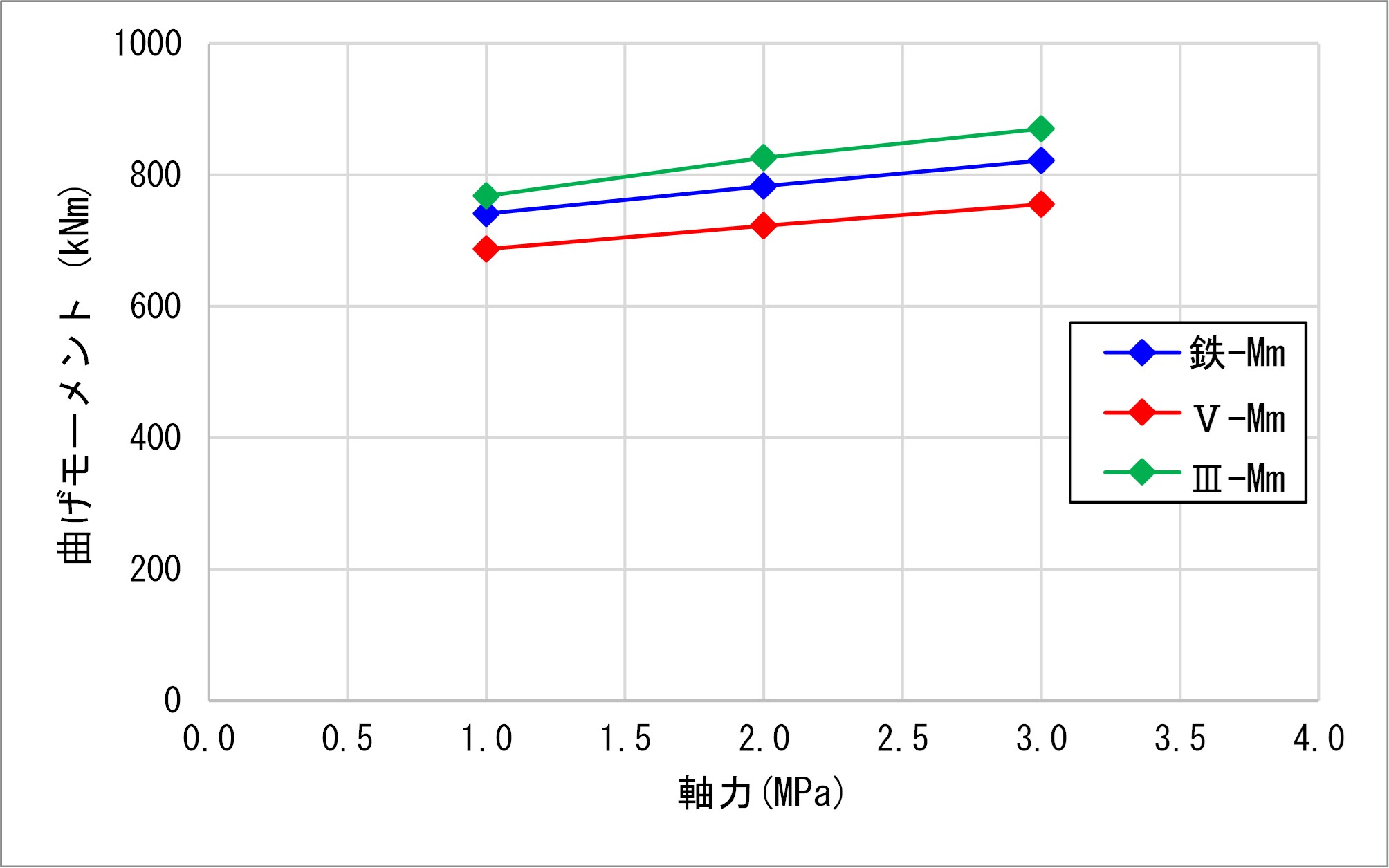
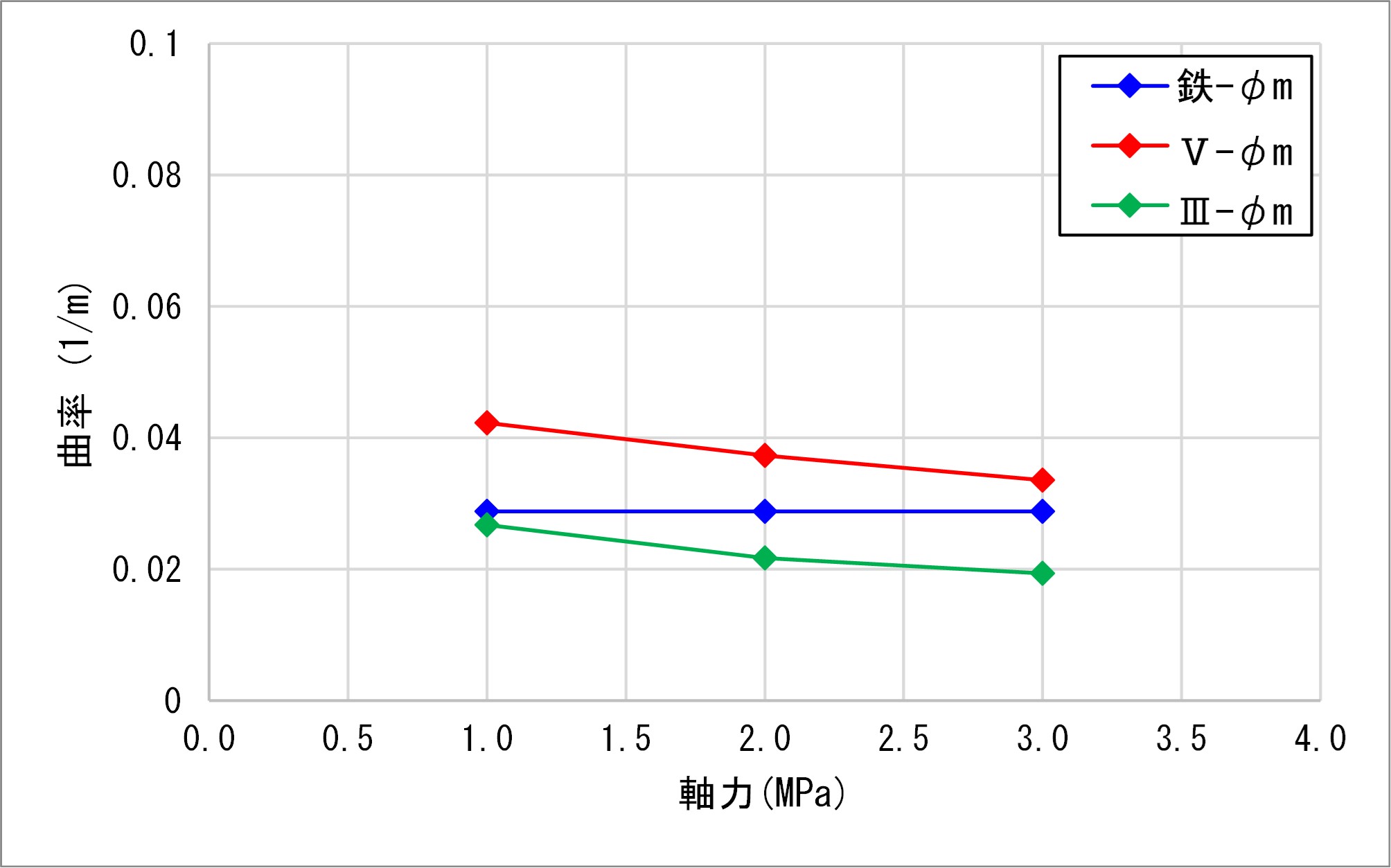
　最大曲げモーメントM_mは道示Ⅲ＞鉄道標準＞道示Ⅴとなり、曲率φ_mは道示Ⅴ＞鉄道＞道示Ⅲとなり、M_mの結果と逆になりました。
　鉄道標準の曲率φ_mは軸力に影響されないため、低軸力下で比較すると道示Ⅲに近く、高軸力下で比較すると道示Ⅴに近くなりました。
　同軸力時では、最大曲げモーメントM_mより曲率φ_mで各基準および軸力による差が大きくなります。
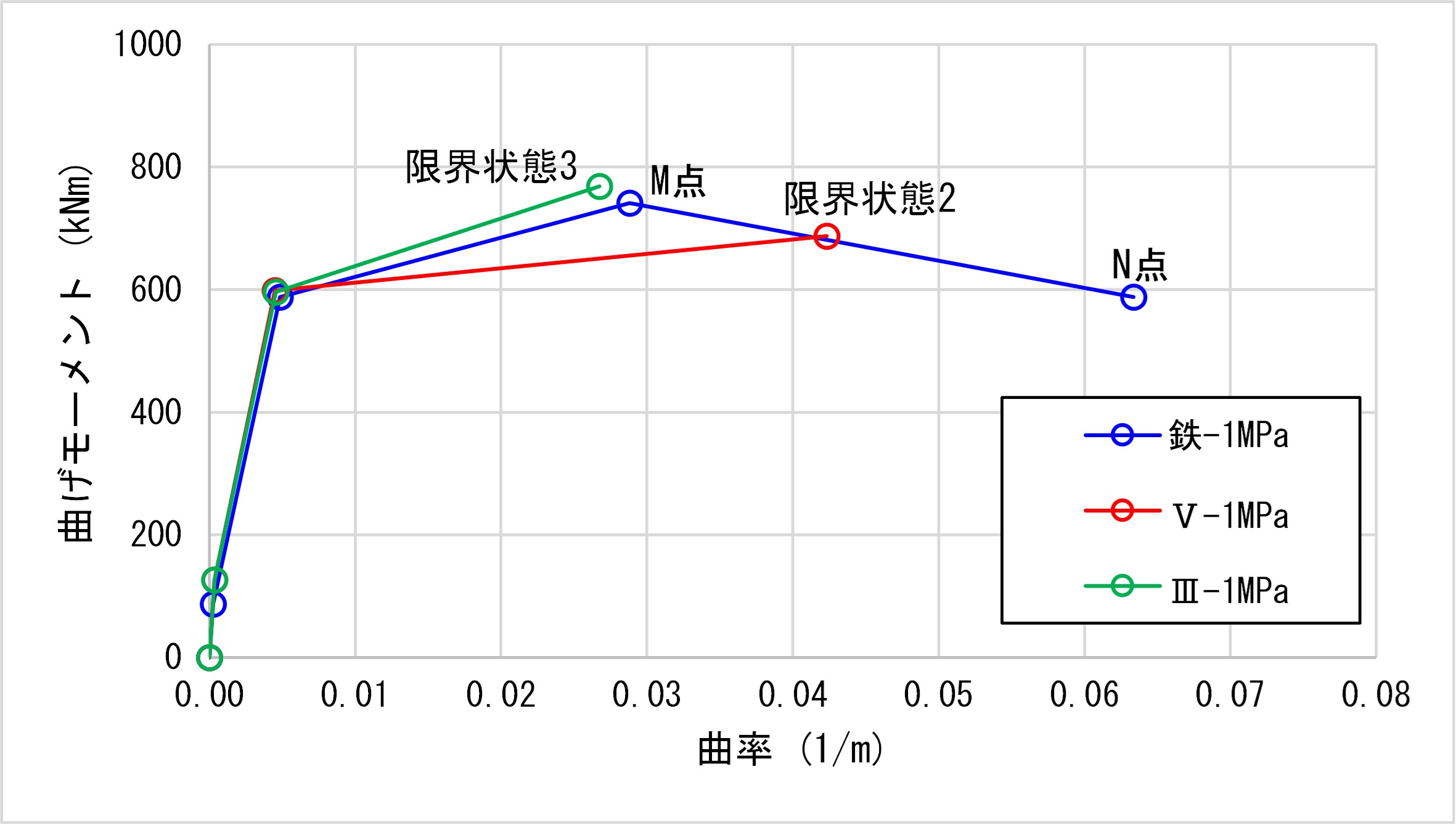
　例えば、最大曲げモーメントM_mの比率（道示Ⅴと道示Ⅲ）は15％程度の差で、曲率φ_m（道示Ⅴと道示Ⅲ）の73％程度となります。図22に1MP_a時の各基準によるM-φ関係を示します。

図22　三基準のM-φ関係比較（1MPa）

　次回は軸方向鉄筋の伸び出しを考慮したM-φ関係の算出、動的解析モデルへ適用方法、影響等を検証したいと思います。

参考文献