振動実験に用いる相似則
解析全般 2022.09.211.はじめに
地盤・構造物連成系の振動性状あるいは破壊性状を検討するとき,遠心力載荷,振動台実験等による模型実験が実施されることがあります。模型実験では,実大スケールの構造物を扱う必要がなくなるため,環境の制約を受けず様々な現象の再現が可能となるものの,模型の挙動から実物の応答が推定できるよう,これらの間に成立する相似則を適切に考慮しなければなりません。本レポートでは,振動台模型実験における相似則の考え方と適用に関する留意点を報告することとします。
2.相似則とは
任意の重力場を考慮できる遠心力載荷実験とは異なり,実地盤と模型地盤で同一の1G場の重力加速度を与える振動台実験では表-1に示す相似則が用いられます。これは,香川1),国生,井合によって提案されているものであり,模型において実物と同じ土,同じ重力場が用いられたときに,全ての応力は1/λに,そして全てのひずみは1/√λに縮尺されることとなり,この場合振動数はλ3/4となります。したがいまして,表中の時間縮尺に準じ,入力地震動の時間刻みを1/λ3/4に短縮する処理が必要となります。

3.解析概要
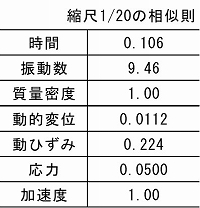
表-2に示す拘束圧依存を考慮した深さ20mの実地盤と深さ1mの模型地盤の2種類の土柱モデルに対し全応力解析を実行し,比較検討を行います。地盤の非線形性はROモデルを使用します。また,模型縮尺1/20の相似則を表-2に示します。なお,土の単位体積重量は20kN/m3とし,実地盤モデルは中心位置でせん断弾性波Vs=190m/s,等価固有周期Teq=が0.42秒,模型地盤モデルはVs=90m/s,Teq=が0.045秒を想定しています。
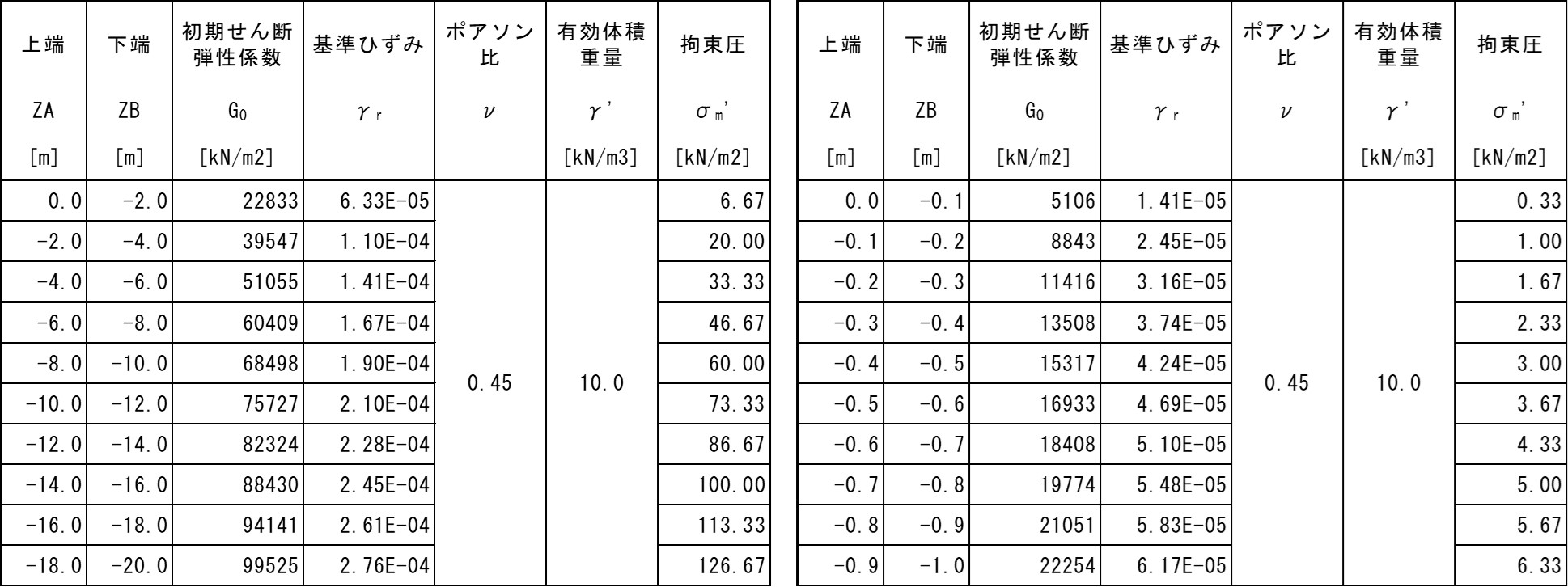
実地盤モデル,模型地盤モデルともhmax=0.24
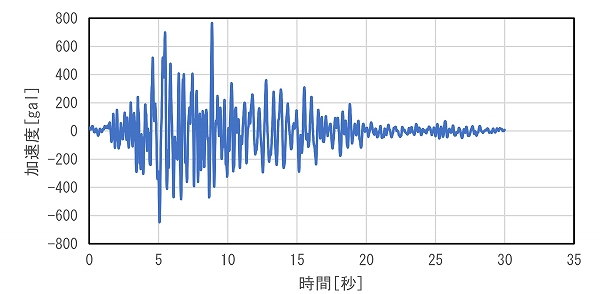
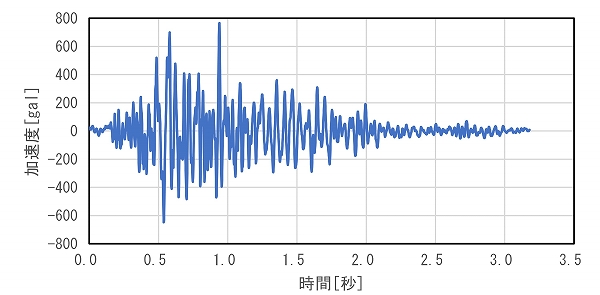
地震動は道路橋示方書の規定波の図-1に示すⅡ-Ⅰ-1波を使用し,モデル底面の固定境界から入力します。一方,模型地盤はⅡ-Ⅰ-1波の時間刻み0.01秒に表-3の時間縮尺0.106を乗じて処理した図-2に示す波形を入力します。
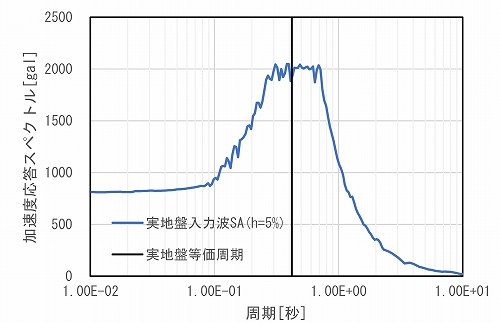
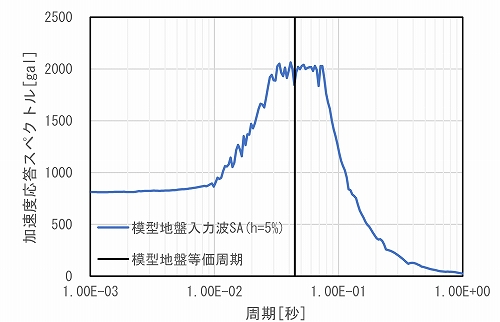
図-3,図-4に入力地震動の加速度応答スペクトル(h=5%)を示すします。図に示す通り,表-3の時間縮尺を考慮することにより,実地盤と模型地盤のそれぞれの固有周期の加速度スペクトルが整合することが確認できます。
ここで注意が必要なのが減衰の与え方です。
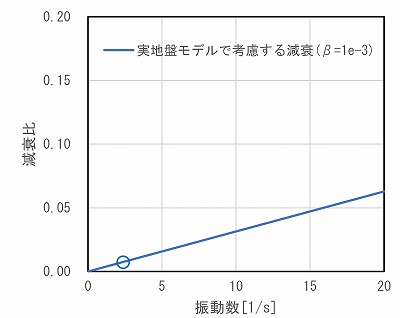
地盤を対象とした非線形時刻歴応答解析でよく用いられる剛性比例減衰(C=β[K])のβ=0.001を実地盤モデルで考慮します.この場合図-5に示すように,等価固有振動数2.38Hz(=1/Teq)でh=0.7%程度の減衰を考慮することになります。この設定を等価固有振動数22Hzの模型地盤にそのまま転用すると,およそ10倍の減衰が考慮されてしまうため,図-6のように実地盤モデルの1/10のβ=0.0001とします。
4.計算結果
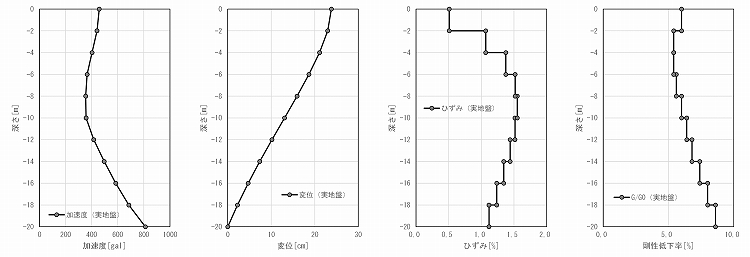
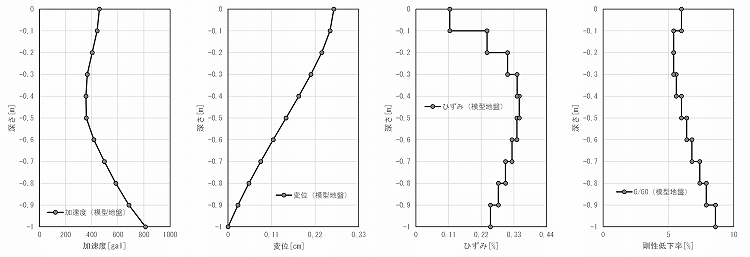
最大応答値を図-7に示します。あえて実地盤換算せず,計算結果をそのままプロットしています。ひずみに依存した剛性低下率は実地盤モデルと模型地盤モデルで一致し,表-3の相似則の通り,加速度は模/実=1,変位は模/実=0.011,ひずみは模/実=0.22であることが確認できます。
5.まとめ
振動台実験で模型モデルを設定する際は,相似則にしたがって時間刻みを処理した入力地震動を使用し,適切な剛性比例減衰を考慮することで,実地盤モデルを高精度で再現できることを確認しました.
参考文献
1)香川崇章:土構造物の模型振動実験における相似則,土木学会論文報告集,第275号,pp.393-396,1978