今回は横倒れ座屈について紹介します。

1．はじめに

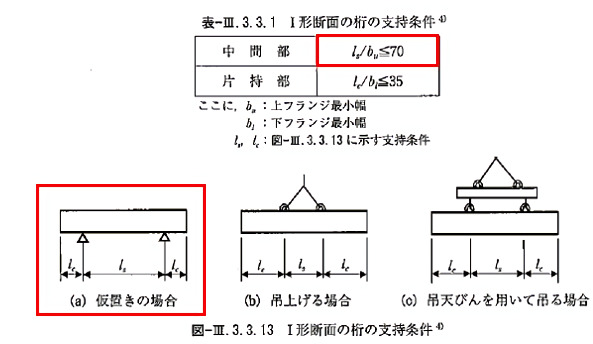
 細長くフランジ幅の狭いＩ桁は、水平曲げ剛性ならびに捩り剛性が低いため、単材での仮置き・吊上げ時に横倒れ座屈の懸念があり、2本以上の桁を箱形に地組して対処することが多い。架設検討では，図-1に示すフランジ幅と支間長で計算される簡易式で安全性を確認することが一般的であるが、本レポートでは、桁の横倒れ座屈問題について、線形座屈解析で得られる限界荷重と幾何非線形解析の荷重分岐点の整合性を確認した。

図-1 横倒れ座屈を防止するためのＩ桁のフランジ幅・支間長比（鋼道路橋施工便覧R2.9日本道路協会）

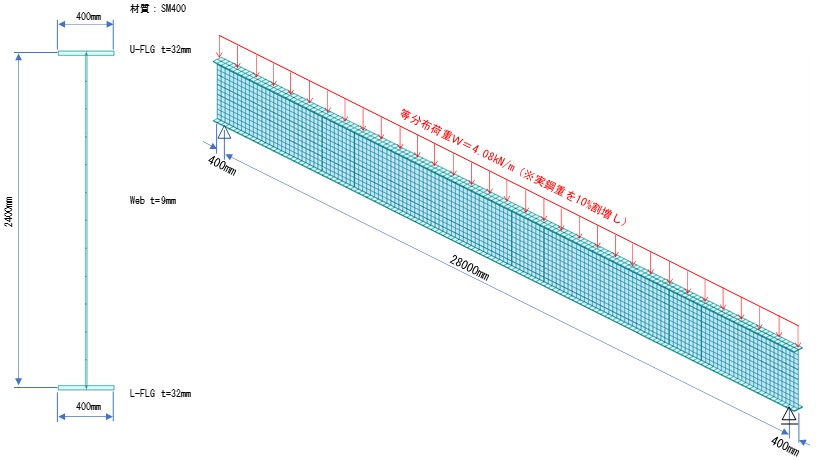
 解析モデルは、寸法および荷重は図-2に示すシェル要素で構成するものとする。なお、図-1に示すフランジ幅・支間長比を目安にフランジ幅400㎜、支点距離28ｍとした。

図-2 解析モデル図

２．線形座屈解析

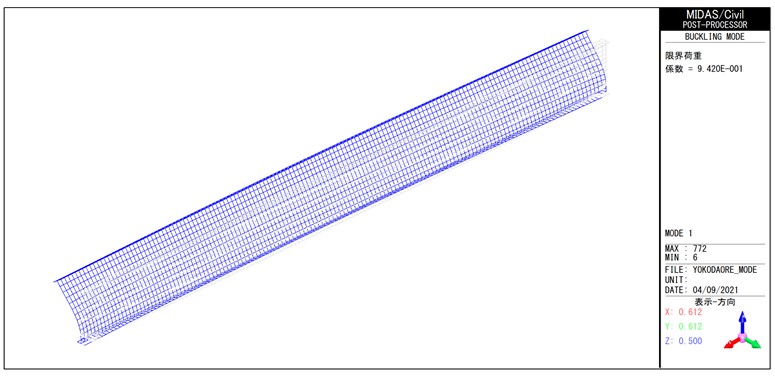
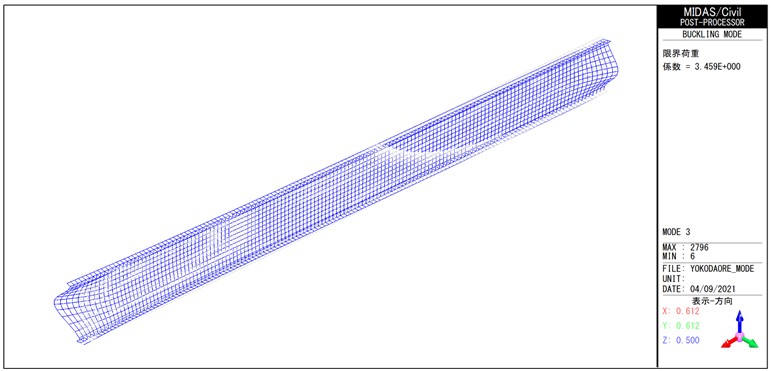
 MidasCiVilによる線形座屈解析（４次モードまで）の結果を図-3～図-6に示す。  図-3の１次座屈モード図に示す通り、荷重係数は0.942となり、本計算で設定した荷重強度は横倒れ座屈が発生する限界荷重とほぼ同等であることがわかる。

図-3 座屈モード（1次）

図-4 座屈モード（2次）

図-5 座屈モード（3次）

図-6 座屈モード（4次）

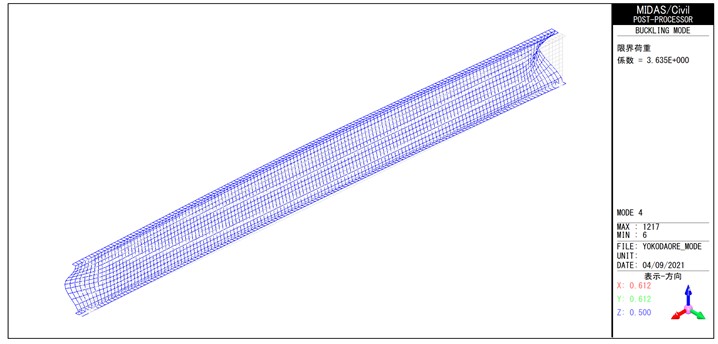
３．幾何非線形解析

 先述の図-2の解析モデルならびに鉛直方向の等分布荷重を使用し、さらに図-7に示す微小な攪乱力を考慮した幾何非線形解析を実施した。なお、荷重増分は５０分割とし、収束法はニュートンラフソン法（変位ノルム比0.0001以下）とした。

図-7 幾何非線形解析で考慮する攪乱力の作用位置

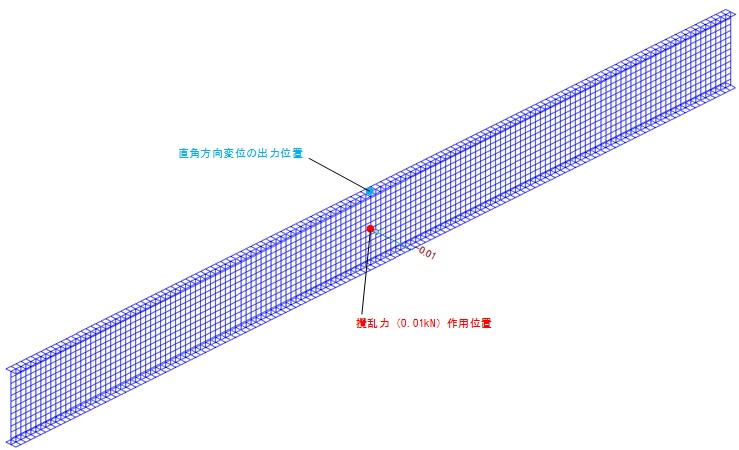
 MidasCivilによる幾何非線形解析で得られた変形図を図-8～図-13に示す。

図-8 荷重比0.80における変形図（倍率：実寸×300）

図-9 荷重比0.90における変形図（倍率：実寸×300）

図-10 荷重比0.92における変形図（倍率：実寸×300）

図-11 荷重比0.94における変形図（倍率：実寸×300）

図-12 荷重比0.96における変形図（倍率：実寸×15.92 ※自動）

図-13 荷重比0.98における変形図（倍率：実寸×6.345 ※自動）

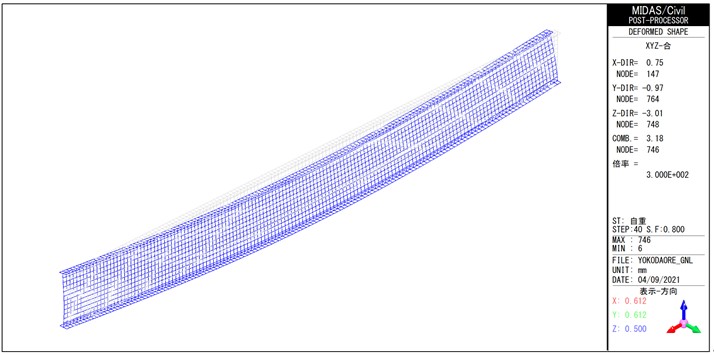
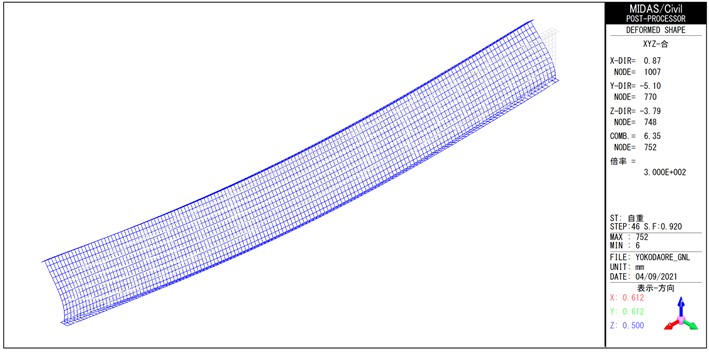
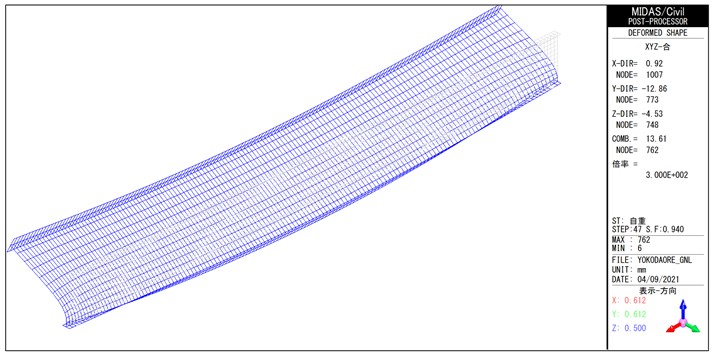
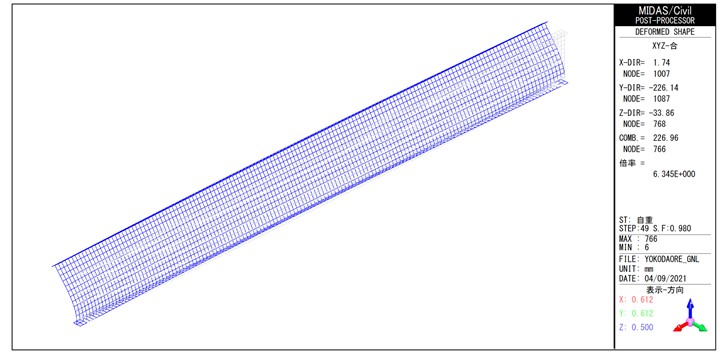
 幾何非線形解析による荷重―直角変位関係を図-14に示す。

図-14 幾何非線形解析による荷重-直角変位関係

 平衡が不安定となる分岐点は荷重比0.94であった。

４．まとめ

    線形座屈解析による限界荷重 ：荷重比 0.942
    幾何非線形解析による分岐点 ：荷重比 0.94

 線形座屈解析と幾何非線形解析の異なる計算アプローチで同等の臨界荷重を確認できた。
 今回はＩ桁１種類の形状で座屈解析を実施したが、次の機会では様々な桁形状、あるいは桁間隔の狭い２主桁形式に対する横倒れ座屈の傾向について考察したい。