スロッシング解析
解析全般 2021.05.28今回はスロッシング解析について紹介します。
1.スロッシングによるタンクの地震被害
1964年の新潟地震、1983年の日本海中部地震などで原油タンクのスロッシングによる被害が報じられたが、2003年9月の北海道十勝沖地震(マグニチュード8.0)では、苫小牧の製油所において、長周期地震動による浮き屋根の揺動・破損ならびに沈没後、国内で初めてのナフサタンクの全面火災が発生し、当時、地域住民への多大なる不安、ならびに大きな社会的注目を集めることとなった。

9/28 16:51 上空南部から撮影
2.速度ポテンシャル理論
スロッシング検討の際、実務において一般的に用いられる固有周期、液面上昇量の算定式を以下に示す。
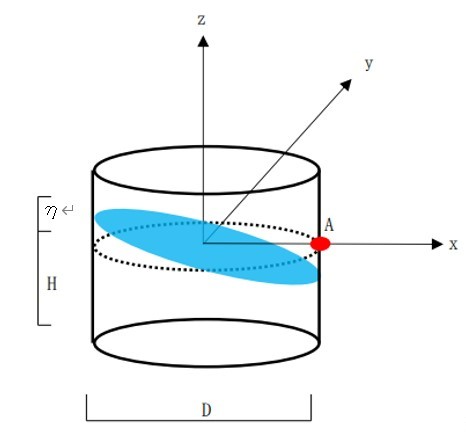

D:タンク直径 [m] H:タンク液高 [m] g :重力加速度 [m/s²] Ts:スロッシング固有周期 [s] Sv:速度応答スペクトル [m/s] η:液面上昇量 [m]
十勝沖地震で最も被害の大きかった“30063ナフサタンク”の形状寸法に対し、既往強震記録を代表する道路橋示方書Ⅴ編に規定している標準加速度波形2波(以降、“神戸波”と“十勝波”と呼称)の速度スペクトルを適用した場合の結果を下表に示す。

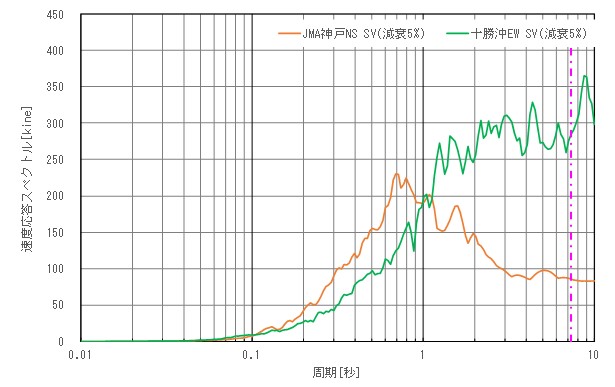
使用した道路橋示方書の標準加速度波形を図-2、図-3に示す。
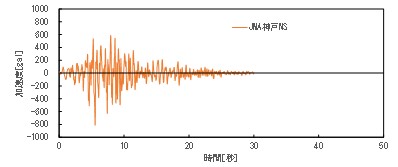
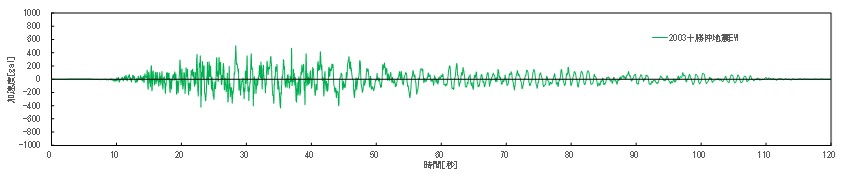
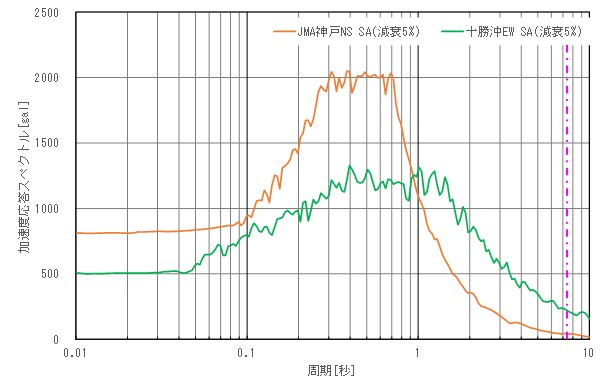
使用した道路橋示方書の標準加速度波形の加速度応答スペクトルおよび速度応答スペクトルを図-4、図-5に示す。加速度のピークスペクトルは神戸波が2000galと十勝波の1250galに対し大きく上回るが、1.0秒を越える長周期帯のスペクトルは大小関係が逆転し、対象のスロッシング固有周期の7秒における十勝波の速度応答スペクトルは神戸波の2倍以上であることが分かる。
3.シミュレーション解析
下図の3次元モデルで液体・構造物連成解析を実施した。
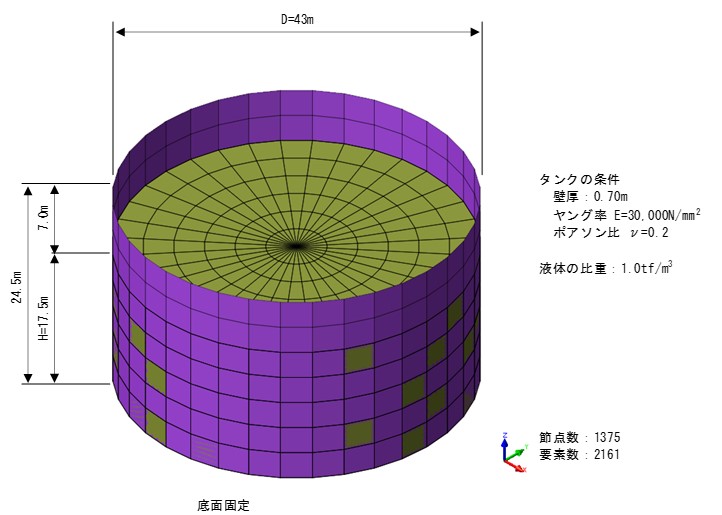
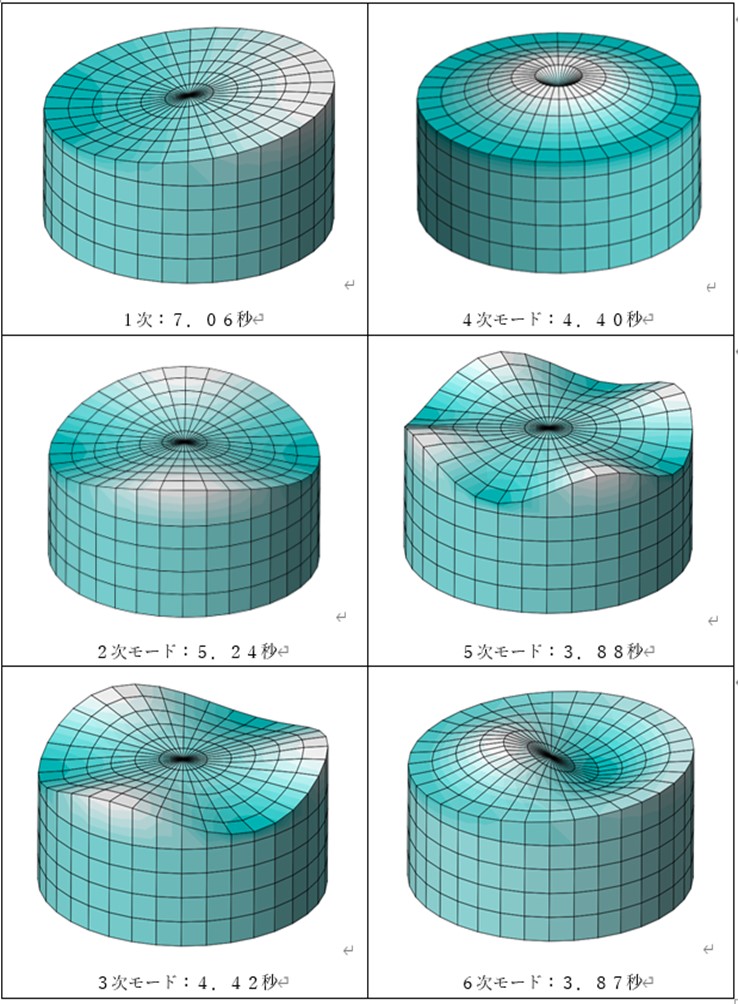
なお、計算プログラムは、非粘性・非圧縮液体を仮定した液体圧力を用いたオイラー法による運動方程式を用いることで液体・構造物連成問題を定式化したSoilPLUSを使用した。代表的なスロッシング固有モードを図-7に示す。速度ポテンシャル理論での固有値計算式で7.21秒、3次元モデルの連成解析で7.06秒と概ね同等の結果が得られた。
次に解析モデルの下端に前述の神戸波および十勝波をX方向に動的に入力した。解法はモード法応答解析を使用し、全てのモード次数で減衰5%を考慮した。図-8、図-9に液面上昇量最大時の変形図を示す。
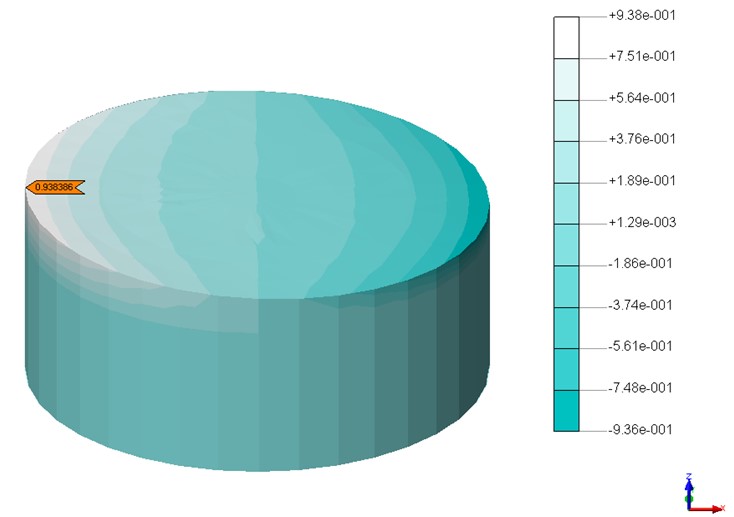
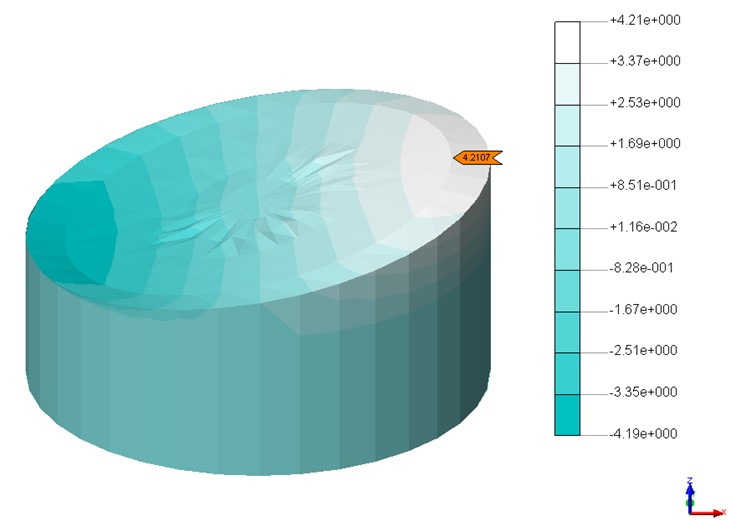
図-10に十勝波の時刻毎変形図を示す。

中心部でのアワグラス変形は、今回の円筒形モデルに対する要素分割を放射状にした影響で、中心部の要素形状が低クオリティになったことが原因と考えられる。また、図-10の45秒時に右側の液面が上昇すると、左側の壁面を押す側の水圧の影響でタンクは左側に変形し、48秒で反転していることが確認できる。下図に液面上昇量の時刻歴応答図を示す。
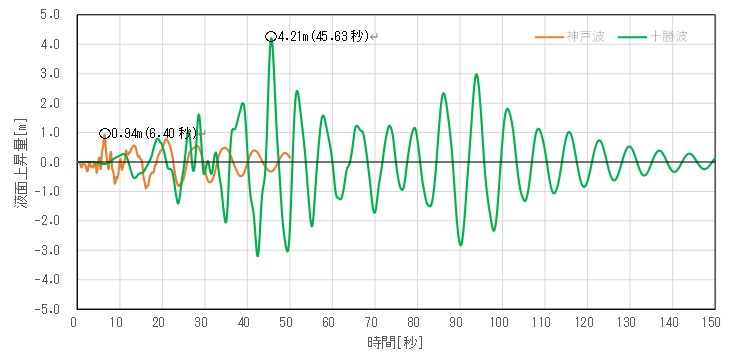
神戸波、十勝波はそれぞれ30秒、110秒で入力波の加速度振幅が収束しているが、その後、液面は数十秒にわたり長周期で揺動していることが確認できる。
4.まとめ
速度ポテンシャル理論の計算式によるスロッシング固有周期ならびに液面上昇量を3次元FEM解析で概ね再現できたが、解析による神戸波での液面上昇量がやや低目の結果となった点、ならびに十勝波での液面中心部での応答の乱れは、中心部の要素分割の影響が考えられ、次回のレポートではメッシュ形状を改善したモデルでの検証を行いたい。
