過去のコラム(Vol.8　軸対称モデルの解析)にて軸対称解析と３次元解析の比較について検証を行った。

今回はより軸対称解析に近いモデルということで円筒型の３次元モデルで比較を行い、分割数による精度の違いについて検証を行った。

解析モデルを図1-1、1-2に示す。
解析モデルは掘削範囲を幅６m、深さ１０mとして半断面（3Dは1/4断面）をモデル化した。また、地盤は１層モデルとした。

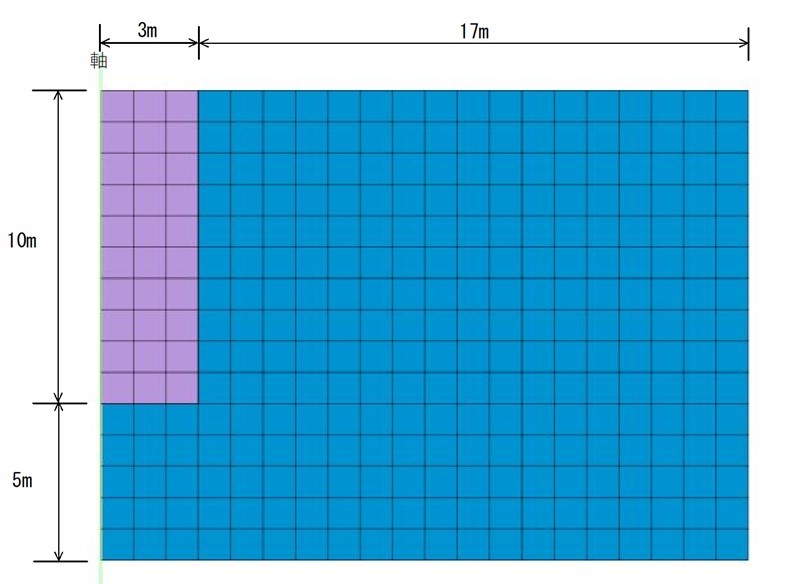
図1-1　軸対称モデル

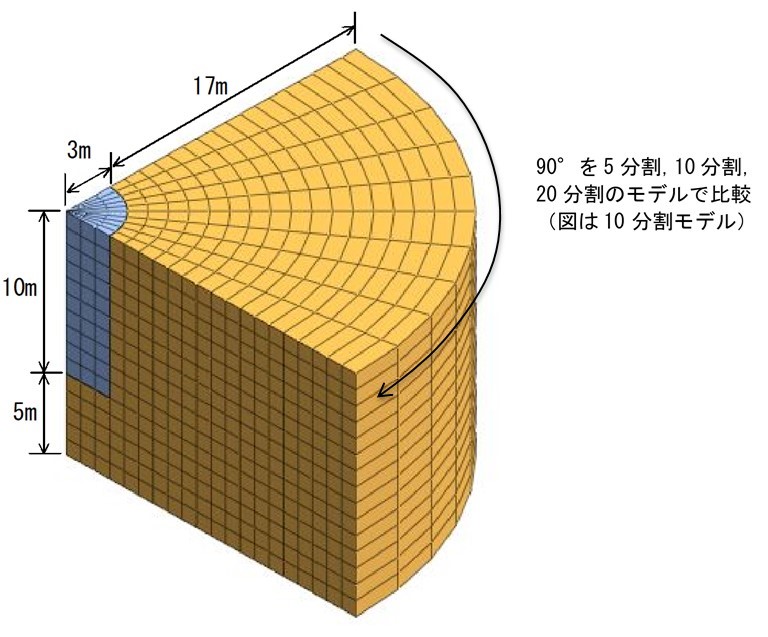
図1-2　３次元モデル

地盤物性値を図2に示す。

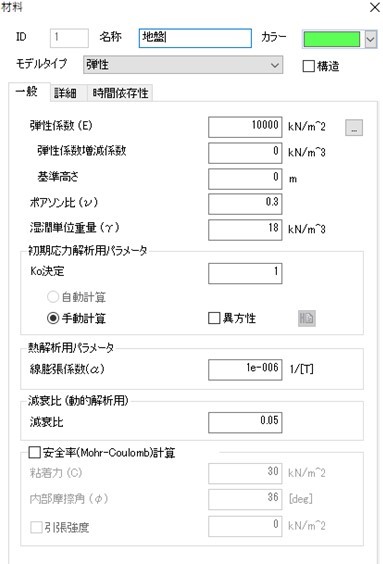
図2　地盤物性値

CASE1　軸対称解析
図3-1に示す範囲を掘削する解析を軸対称解析で実行する。

図3-1　軸対称解析（掘削）

CASE2　３次元解析（５分割）

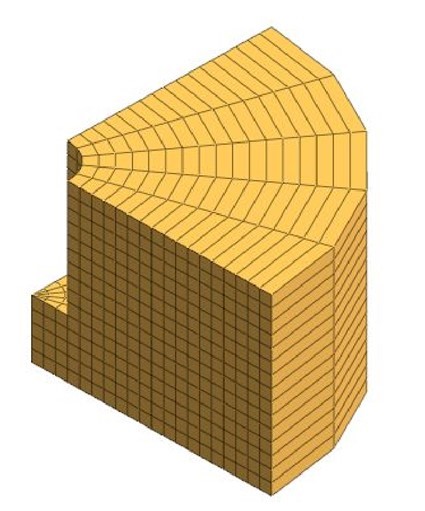
図3-2　３次元解析（5分割）

CASE3　３次元解析（10分割）

図3-3　３次元解析（10分割）

CASE4　３次元解析（20分割）

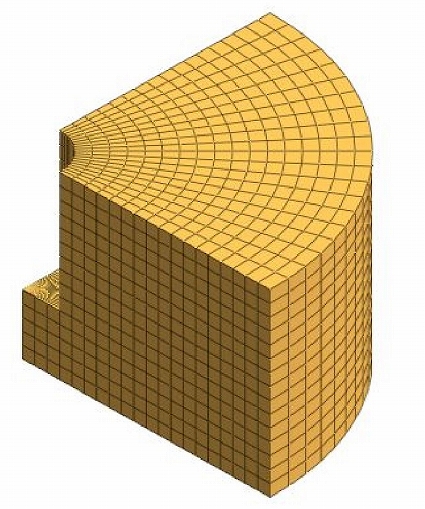
図3-4　３次元解析（20分割）

CASE1　軸対称解析

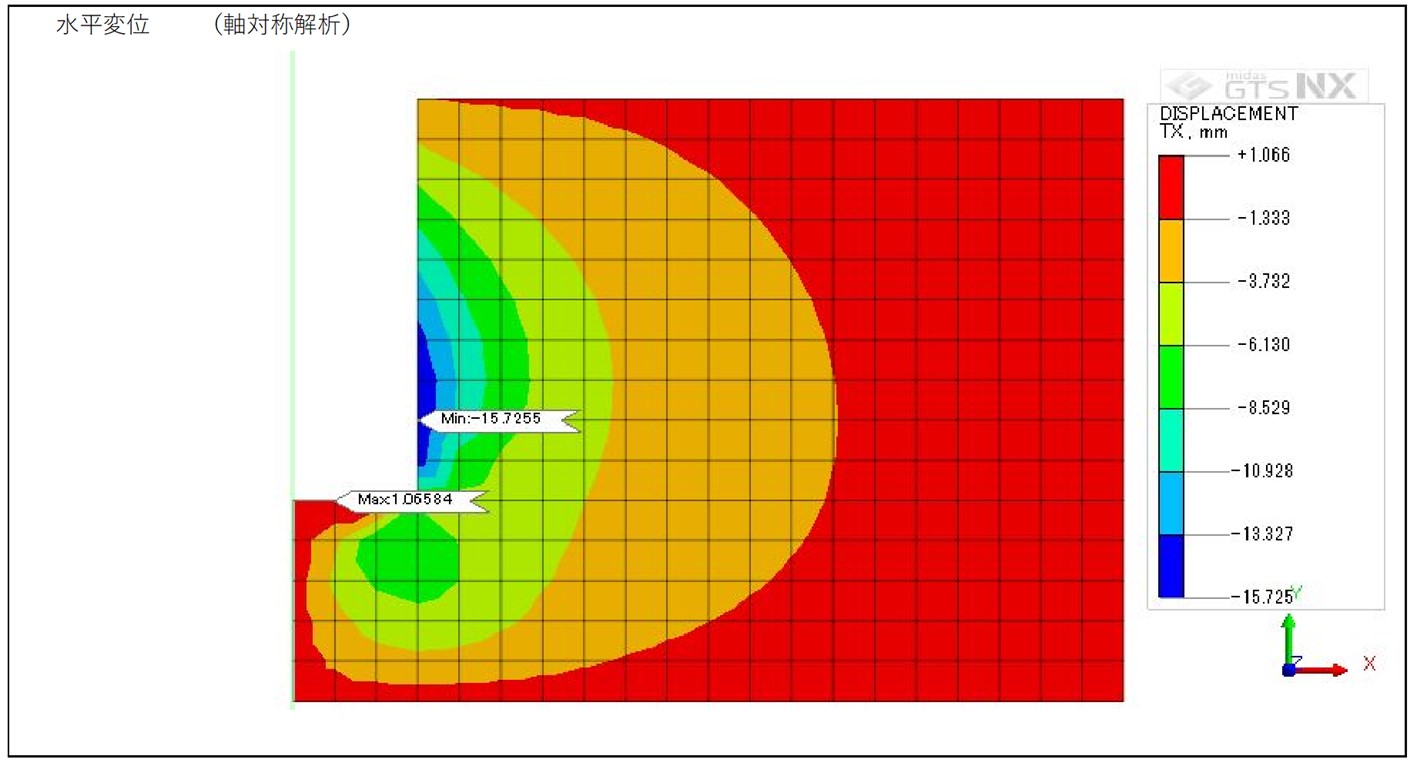
図4-1-1　軸対称解析　水平変位コンター図

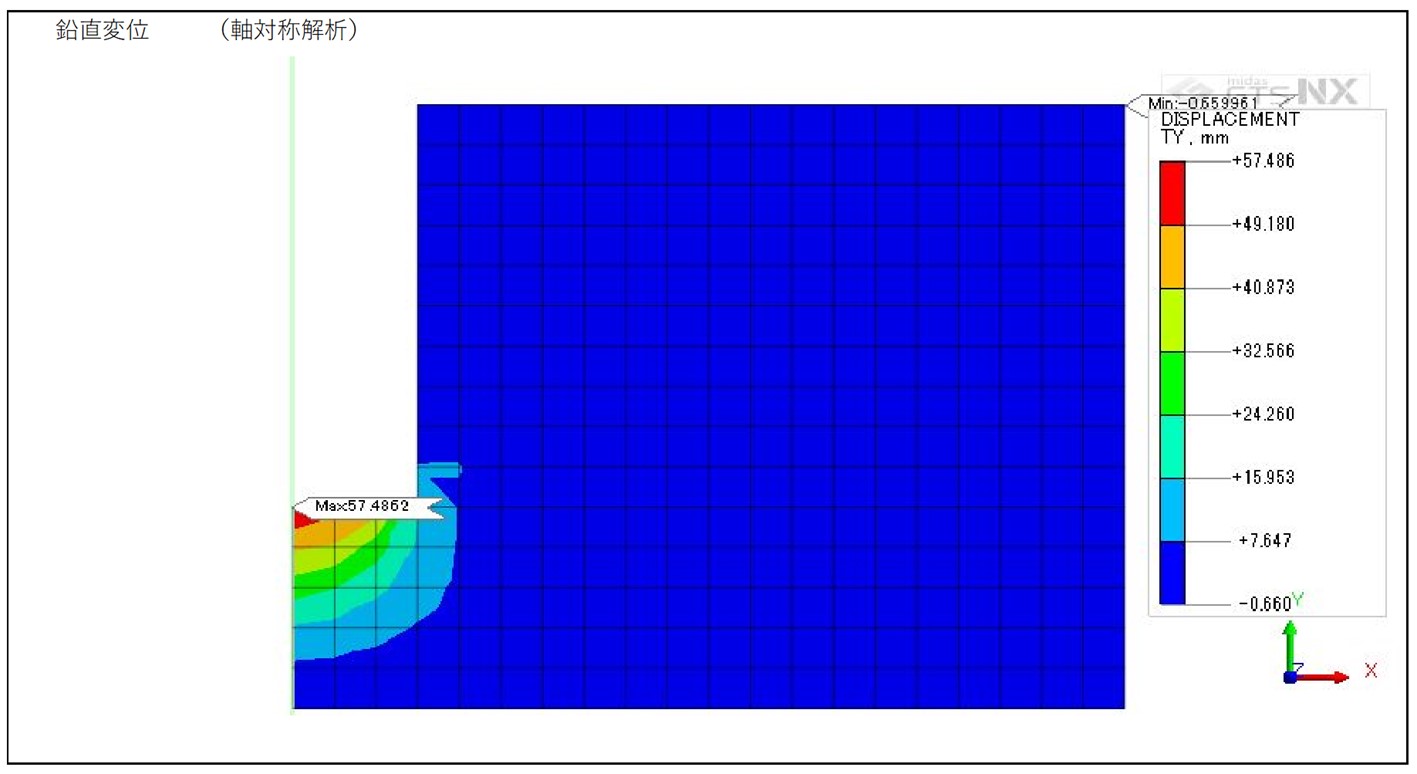
図4-1-2　軸対称解析　鉛直変位コンター図

CASE2　３次元解析（5分割モデル）

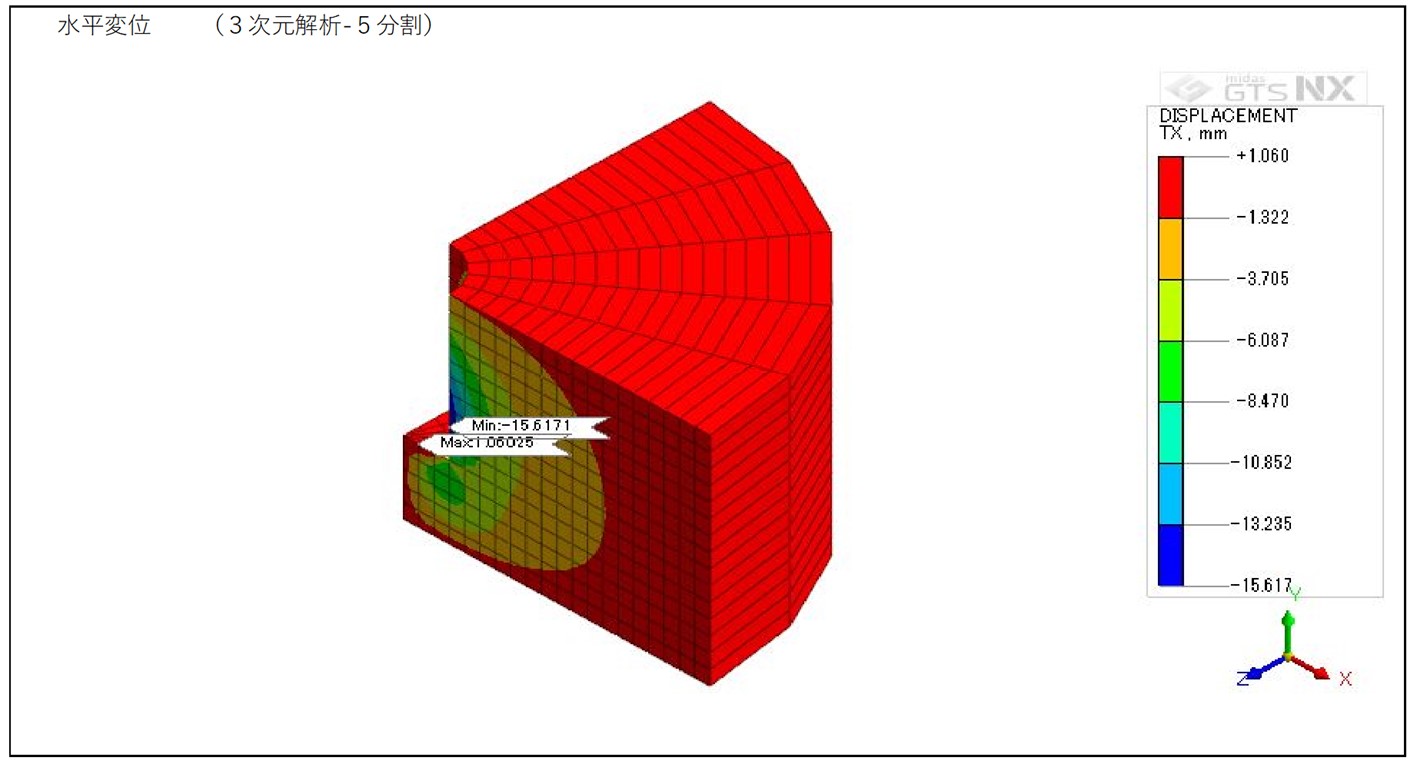
図4-2-1　5分割モデル　水平変位コンター図

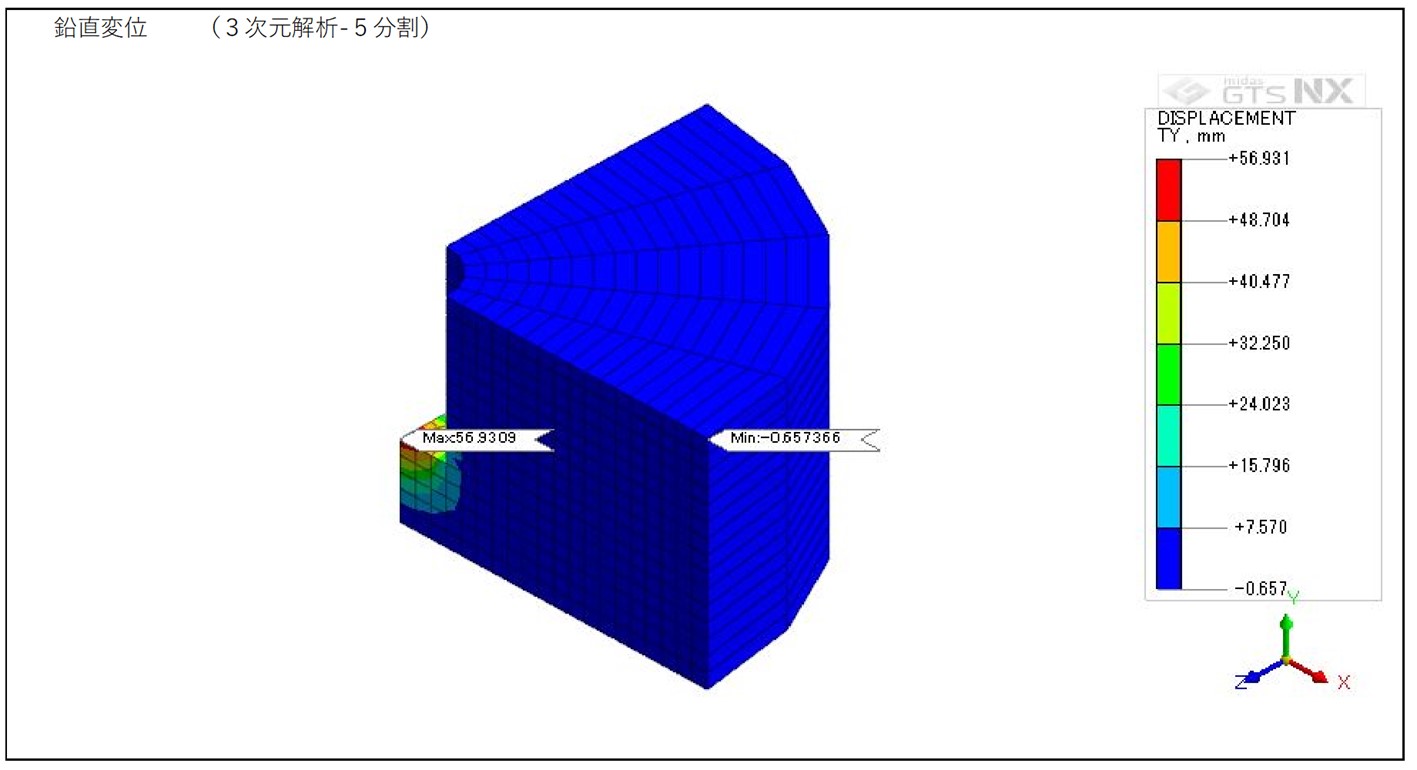
図4-2-2　5分割モデル　鉛直変位コンター図

CASE3　３次元解析（10分割モデル）

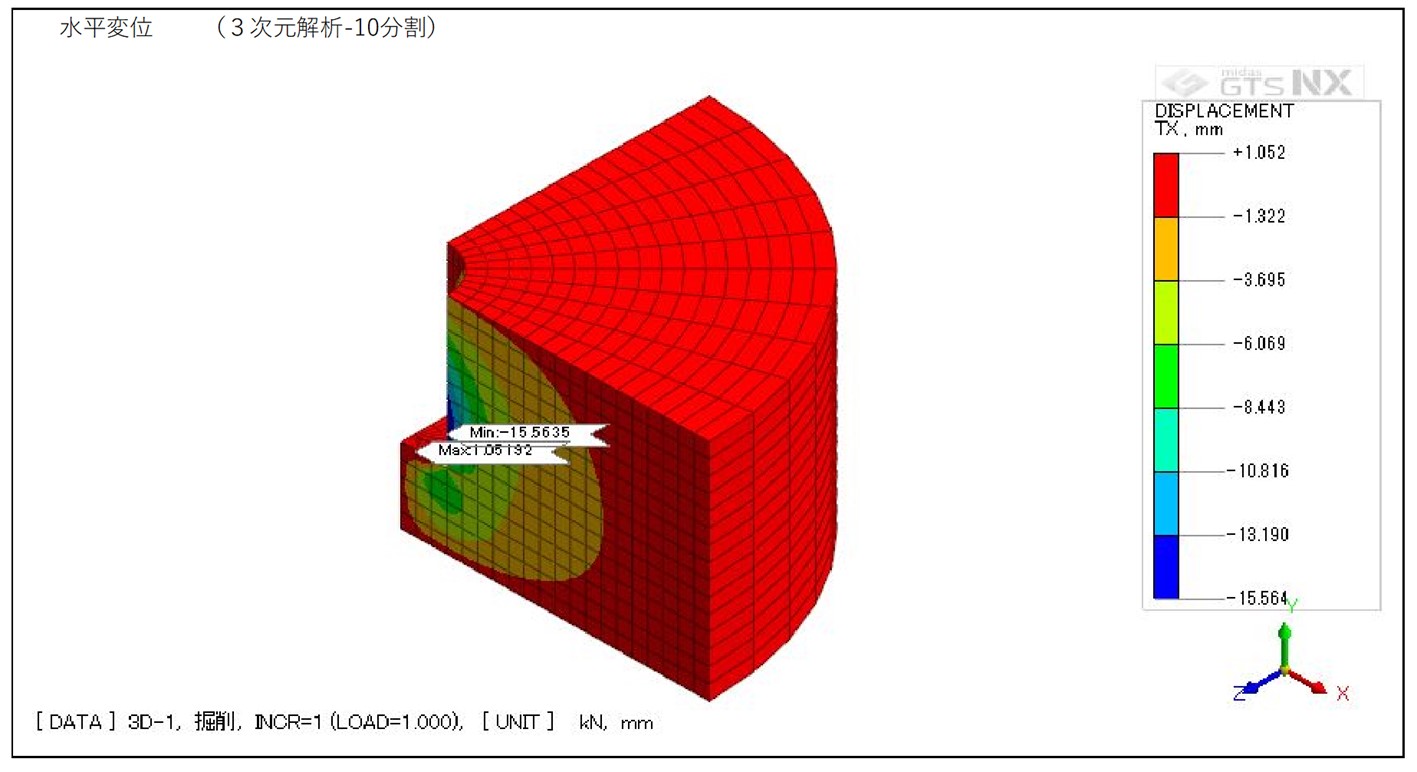
図4-3-1　10分割モデル　水平変位コンター図

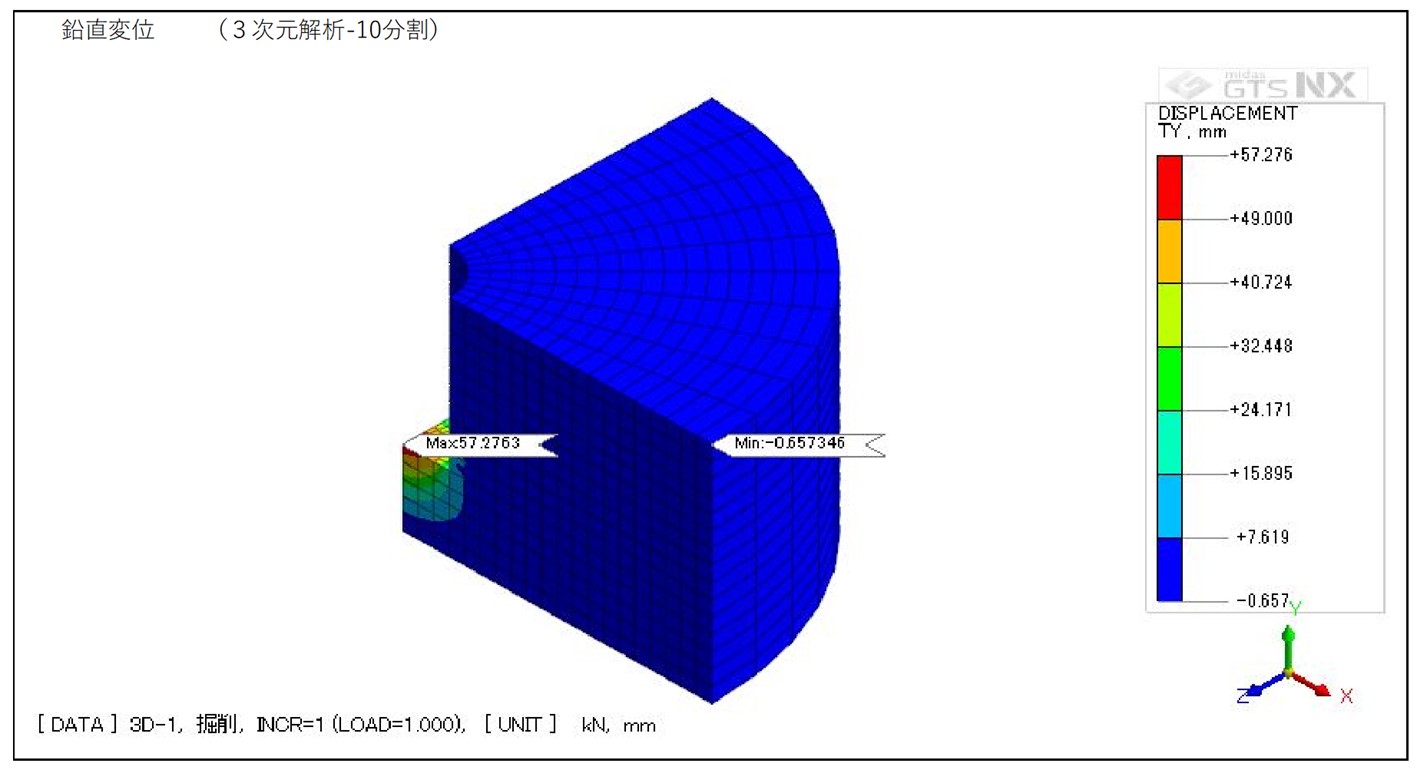
図4-3-2　10分割モデル　鉛直変位コンター図

CASE4　３次元解析（20分割モデル）

図4-4-1　20分割モデル　水平変位コンター図

図4-4-2　20分割モデル　鉛直変位コンター図

・軸対称解析と3次元解析の変位比較

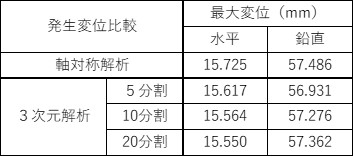
軸対称解析と３次元解析の比較では概ね同じ結果であるが、３次元解析の方が変位量が小さい結果となった。
３次元モデルの分割数については大きな違いはないが、水平変位は分割数が粗い方が軸対称解析の結果に近く、鉛直変位は分割数が細かい方が軸対称解析の結果に近くなった。
今回の検証結果を踏まえて次回は荷重条件による比較や梁要素を用いた比較など行いたい。