（１）はじめに
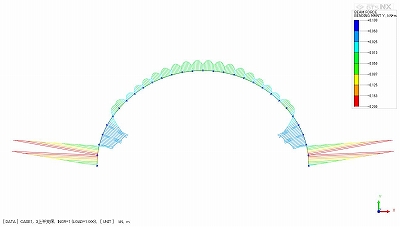
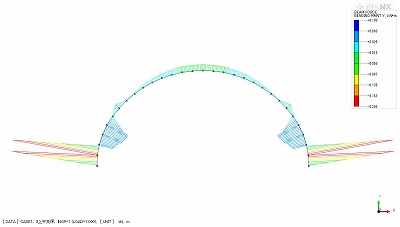
　かなり特殊なケースですが、トンネルの掘削解析において、支保工をモデル化した梁要素の曲げモーメント図を描くと、曲げモーメントが、図-1のアーチ上部のように、凹凸の激しい図になることがあります。
　なぜ、このような図になるのかを考えてみました。

図-1　支保工のモーメント図（ロックボルト無し）

　FEM解析における梁要素を構造の面から考えますと、梁要素と平面(3次元の場合はｿﾘｯﾄﾞ)要素は節点で結ばれていますが、節点間（要素の辺の部分）では平面要素はフレーム解析における分布バネのような作用はしません。
　しかし、荷重の面から考えますと、本解析で使用しているmidas NXではフレーム解析と同様に、梁要素の節点間に集中荷重を作用させたり、等分布荷重や不等分布荷重を作用させたりすることができます。したがって、梁要素の自重を作用させますとその自重によって生じる曲げモーメントは2次関数分布になります。
　（midas NXでは、梁要素に荷重を作用させる場合は「梁要素荷重」を使用します。）
　ここで、掘削解析の場合は、掘削解放力は節点に作用させるので、梁要素から考えると両端の節点に集中荷重が作用し、分布荷重では作用しません。
（２）検証解析
　わかりやすく簡略化した例を用いて検証してみます。
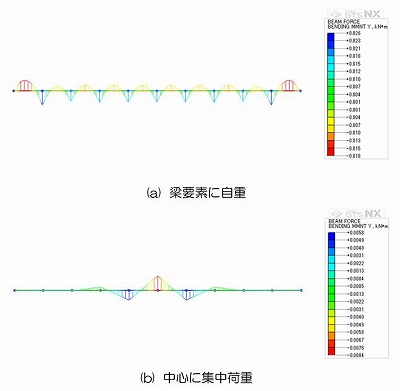
　図-2は、地盤を模した平面要素を1要素だけ作成し、その下部に梁要素を並べたモデルです。(a)は荷重として梁要素の自重を作用させ、(b)は、掘削解放力の代わりにモデル中心の節点に集中荷重を作用させました。

図-2　検証解析のモデル

　図-3は解析結果における曲げモーメント分布図です。(a)は、1要素内で曲げモーメントが２次曲線分布となっており、(b)は、直線分布となっていることがわかります。
　なお、凡例を見ると、両者において曲げモーメントの値が大きく異なっていることがわかりますが、NXは図を同一スケールで表示することができないため、分布の大きさでその違いを認識することができません。
　図-1において、アーチ部分の曲げモーメント分布が2次曲線で側部が1次分布になっているのは、アーチ部においては掘削解放力の影響が小さく、側部では大きいためと考えられます。

図-3　検証解析のモデルの曲げモーメント図

（３）ロックボルトの影響
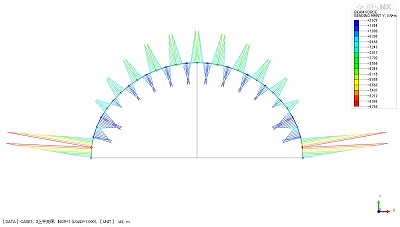
　曲げモーメント図が図-1と異なり、図-4のようになることもあります。図-5を見ていただければわかりますが、これは1節点おきにロックボルトがあるためです。

図-4　支保工のモーメント図（ロックボルト有り）

図-5　支保工のモーメント図（その2）（ロックボルト表示）

（４）ちなみに①
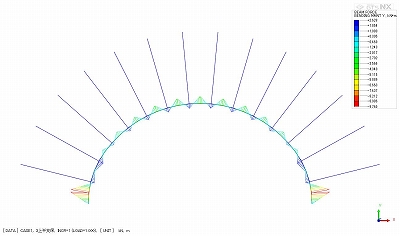
　図-5などで側部の曲げモーメント分布を見ると、まるで1要素内で三角形分布をしているように見えますが、これは要素から鉛直の位置に分布を描いているためで、単なる図化テクニックの問題です。図-5において表示スケールを小さくすると図-6のようになり問題ないことがわかります。

図-６　曲げモーメント分布図（図-5の表示スケールを変更）

（５）ちなみに②
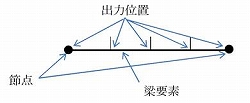
　midas NXでは、梁要素の断面力等の出力位置を出力間隔数※で指定することができます。
　この出力間隔数がデフォルトで4に設定されており、これまでの図はすべて4で出力しています。図-1の解析においてこの出力間隔数を1に変更すると図-6に示す分布図になります。これは図-1の節点での値を用いて曲げモーメントを描いた図になります。我々はこの分布図を見ていることのほうが多いと思います。図-1の出力を避けたい方は、この方法で表示したほうが良いかもしれません。

図-７　曲げモーメント分布図（図-1の梁出力間隔数を1に変更）

（６）おわりに
　実は、図-1のような結果になるケースは、掘削相当外力が極端に小さく、鋼製支保工の自重の影響が卓越するような場合で、通常、掘削相当外力に比べて鋼製支保工の自重の影響はごく小さいので問題になりません。
　したがって、あまり見ることは無いと思いますが、見かけた際は思い出してください。
　※梁要素の出力間隔数
　例えば、出力間隔数が4の場合、下図のように梁要素を4分割した5点で結果値を出力する。出力間隔数が１の場合、出力は両節点の2点となる。

図　梁要素の出力間隔数と出力位置（出力間隔数4の場合）