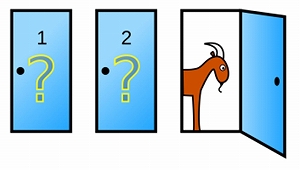
1990年、モンティ・ホールが司会者を務める米国のショー番組の中で、知的好奇心を大いにくすぐられるゲームが行われました。「モンティ・ホール問題」と言われているものです。

　「プレーヤーの前に閉まった3つのドアがあって、1つのドアの後ろには景品の新車が、2つのドアの後ろには、ハズレを意味するヤギがいる。プレーヤーは新車のドアを当てると新車がもらえる。なお、司会者はどのドアが当たりか予め知っている。
　プレーヤーが1つのドアを選択した後、司会のモンティが残りのドアのうちヤギがいるドアを開けてヤギを見せる。
　ここでプレーヤーは、最初に選んだドアを、残っている開けられていないドアに変更してもよいと言われる。プレーヤーはドアを変更すべきだろうか？」（Wikipediaに加筆修正）

　閉まった3つのドアのうち当たりは1つですが、1つのドアがハズレとわかった場合、直観的には残り2枚の当たりの確率はそれぞれ1/2になるように思えます（私もそう思いました）。
　しかし実際には、ドアを変更しない場合の当選確率は1/3、変更した場合は2/3と、変更するほうが2倍の当選確率となります。挑戦者は、確率1/2の2枚のドアのどちらか一つを選んでいるように感じますが、理論的には確率1/3のドアのままにするか、確率2/3のドアに変更するかを選んでいるのです。その理由を簡単に説明すると、いま、新車のドアを●で表すと

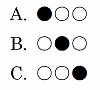
のどれかになります。
　仮に真ん中のドアを選んだとします。B.だけがドアを変更したときにハズレになります。A.とC.は変更さえすれば、必ず●を選択できるように司会者がわざわざ誘導してくれているのです。真ん中のドアを選択していますが、どのドアを選択しても状況は変わりません。
　複数の著名な数学者ですら正解を認められずに激しく反論して、米国中で一時大騒動になりました。

　モンティ・ホール問題は、直観で正しいと思える解答と、論理的に正しい解答が異なる問題の典型的な例です。数学的には、事象A（司会者が一つのハズレのドアを開ける）が起きた上で、事象B（新車が当たる）が起こる確率P(B|A)を求める方法として、「条件付き確率」あるいは「ベイズ推定」と呼ばれています。人の思い込みや、間違った直観と論理や現実との隔たりを排除し、物理現象（事象B）を正しく理解するためには、まず制約条件（事象A）を吟味することが重要であることを示唆しています。

　ところで建設分野では、地震観測記録を活用した地震動予測シミュレーションや液状化リスク分析、水害リスクカーブによる治水対策など、ベイズ推定を工学的に適用した研究がこれまで、多岐にわたって行われています。これらの研究とAIとのコラボレーションは今後、大きな成果をあげてゆくかもしれません。