変位って何?
解析全般 2015.01.29しかし、この変位を現実に正確に測ることは非常に難しいことです。なぜならば、計測の際には、この基準点を仮想的な点ではなく、現実のどこかに取らなければいけないからです。
通常、土木・建築の計測では、工事により変位が生じないと考えられる遠い場所に基準(不動)点をとり、その点を基準(不動)として、計測したい箇所の変位を測ります。しかし、土木・建築の分野ではこの工事が広範囲にわたることが多く、その基準(不動)点を数10mから数100m離れた位置にとらないといけない場合があります。
ここで、問題となるのは、基準(不動)点が遠くなるほど計測精度が落ちることです。数10mから数100m程度離れた点を基準点として、mmレベルの高精度で測るというのは、距離の問題だけではなく、計測点と基準(不動)点の間の障害物の問題もあり、かなり大変です。
筆者は一時土木計測の仕事に携わっており、この時、約450m離れた2点を基準点として、その2点間の各点の変位計測や、約100m×約100m×深さ約20mの掘削工事近接の構造物の変位計測をしたことがありますが、大変な苦労をしました。
距離が長いということの他に、計測期間が数年と長期間となり、生じた変位の解釈の難易度が非常に高くなりました。
これに対し、地盤のFEM解析では、解析変位は絶対変位のように思えますが、実際には、両側端を水平変位拘束、下端を鉛直方向変位拘束とする境界が事実上の基準(不動)点となります。ただし、FEM解析では、境界を好きなだけ遠くに設定できるので、境界を遠くにとれば、絶対変位に近い値が求められると思われがちですが、2次元解析では、境界の位置によって変位結果が大きく異なることがあるため、一概に遠くにとればいいというものでもありません。
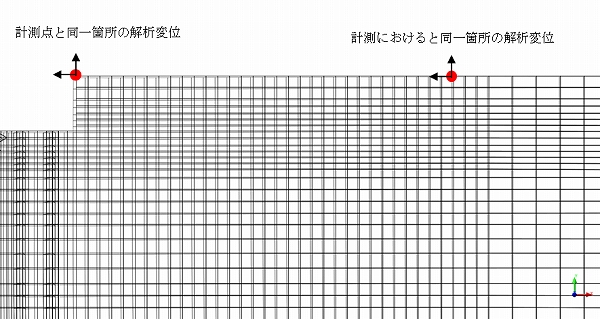
しかし、FEM解析の結果を計測値と比較する場合には、絶対変位にこだわる必要はありません。FEM解析の結果も図のように計測と同一の点に基準(不動)点をとり、その点からの相対変位にしてやれば、計測変位と矛盾なく比較することができます。
皆さんはどう思われますか?
(ご)
