「解析モデルの基本設定」に、「モデルの自重を質量に変換する方向」というのがあります。これは作成した解析モデルの自重を動的解析や固有値解析で必要となる質量に自動的に変換して節点に振り分けてくれるという便利な機能ですが、そこには「集中質量」と「コンシステント質量」があり、「集中質量」には「質量行列に対角成分以外の成分も考慮」が選択できるようになっています。

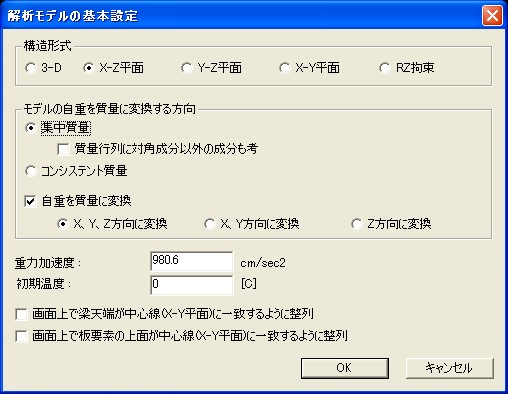
　ちなみに「集中質量」と「コンシステント質量」どちらを選んでもその下の「自重を質量に変換」をチェックしなければ計算してくれません。また、「コンシステント質量」の場合、「ＸＹＺ方向に変換」しか選択できず、「集中質量」の場合は「質量行列に対角成分以外の成分も考慮」にチェックを入れると強制的に「ＸＹＺ方向に変換」となります。ちょっとわかりづらい設定の仕方ですね。
　さて、その前に「構造形式」というのがあって、これは解析の目的やモデルによって設定しますが、３－Ｄは３次元（１節点６自由度）、Ｘ－Ｚ平面は全体座標系Ｘ－Ｚ平面での解析を行います。このときＹ軸方向の変位成分とＸ軸及びＺ軸に対する回転変位成分は自動的に拘束されることになるので、板要素やソリッド要素でモデル化する場合には必要な自由度を拘束しないよう注意が必要です。以上を踏まえて「自重を質量に変換」する方向を選択しましょう。
　それではこれらの設定が動的解析や固有値解析の結果にどのように影響するのでしょうか。簡単なモデルで固有値解析を行ってみました。解析モデルはφ500×14mmの断面を有する高さ10mの鋼管を梁要素でモデル化したものです。支持条件は下端完全固定です。

解析モデル

　質点系モデルなのでＸ－Ｚ平面で解析するものとし、自重→質量の変換は次の３通りとしました。
　①集中質量でＸＹＺ方向に変換
　②集中質量でＸＹＺ方向に変換＋質量行列に対角成分以外の成分も考慮
　③コンシステント質量
　また、以下に示すように、要素分割数も0～10分割としました。

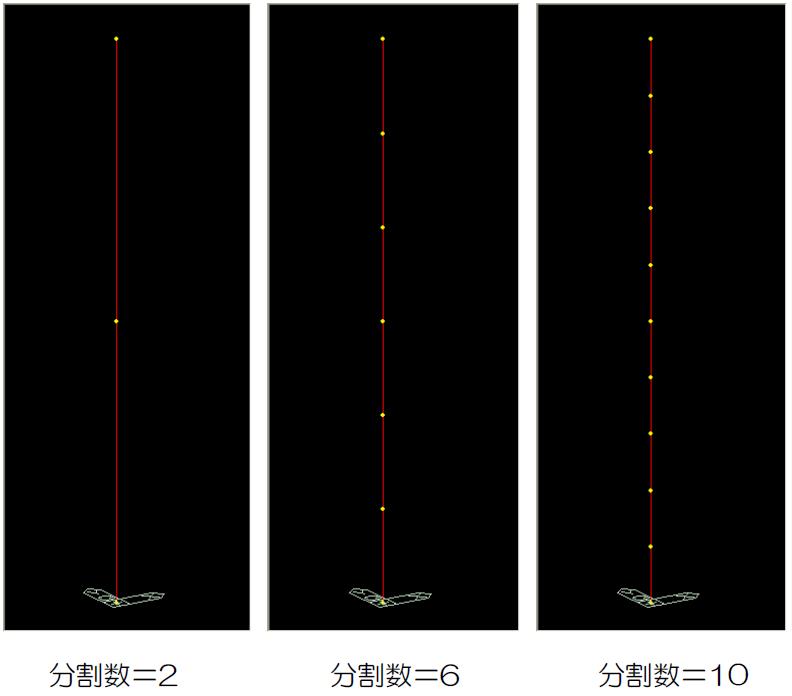　計算の結果得られた一次固有周期をプロットしたのが下図です。横軸は要素分割数です。要素分割数が多いほど精度が良くなるのは当然ですが、コンシステント質量の場合は要素分割数の影響はほとんど無いという結果となっています。ただし、要素分割無しでは高次のモードは算定できませんが。

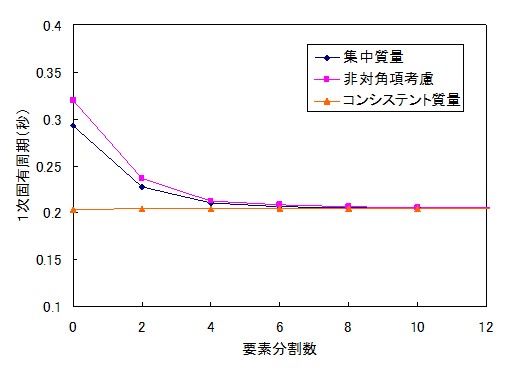
一次固有周期の算定結果（梁要素）

　また出力を見ると、①では１節点に対しＸ、Ｚ方向の２自由度、②、③ではＹ軸周りの自由度が考慮され、３自由度となっていることがわかります。通常の質点系では①としてある程度要素分割すれば十分でしょう。ちなみに①で「ＸＹ方向に変換」とするとＸ方向の結果は同じですがＺ方向の振動モードがなくなります。
　もちろんこの機能を用いなくても個々の節点に質量を与えることができますので、ＸＹＺ方向の質量およびそれぞれの軸周りの回転慣性質量を直接入力して解析することもできます。
　ここで板要素およびソリッド要素を使って同様な計算をしてみました。下図のとおり板要素とソリッド要素のモデルの見た目は同じです。もちろん構造形式は３Ｄとしています。円周方向の分割数を50、高さ方向は同様に0～10分割としました。

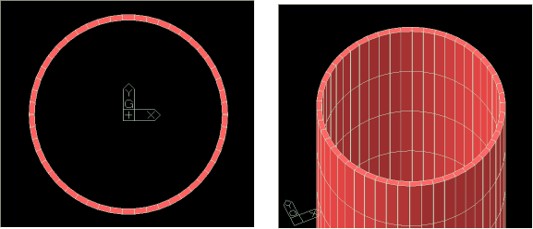
板要素モデル/ソリッド要素モデル

　結果を以下に示します。これによると板要素の場合、要素が6分割のところで少し凸になっていますが梁要素より精度は良さそうです。ソリッド要素の場合も同様な傾向です。なお、板要素、ソリッド要素の場合、「集中質量」と「非対角項考慮」では差がありません。これは各要素の構成節点が回転慣性を考慮していないためと思われます。

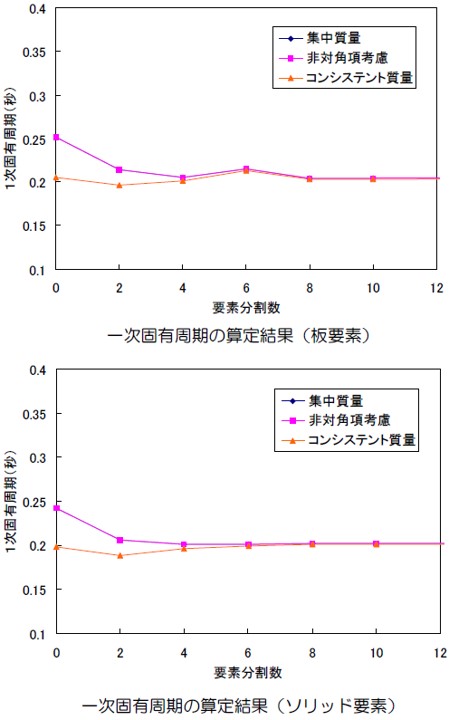
　さて、「正解に近い解」として、それぞれのケースで縦方向の分割数を50とした場合の結果を表-1に示します。これによると一次固有周期は約0.204秒と考えて良さそうです。

　以上、モデルの自重を質量に変換する方法について、計算してみましたが、固有周期を求める場合、最低限必要な振動モードが算定できるような要素分割数をとれば、集中質量であってもコンシステント質量であっても十分な結果が得られそうです。なお、コンシステント質量は固有値解析制御でLanczos法を選択する場合のみ適用可能です。