【はじめに】
　前回では道路橋示方書V¹⁾に示されるコンクリートの応力ひずみ曲線を用いたM-φ計算を矩形断面にて行いました。今回は円形断面で道路協会より公開されている計算例²⁾を再現してみます。

１．計算例（円形）

図-１　検討断面

・断面条件を以下に示します。
　コンクリート強度　　　　30N/mm²
　鉄筋強度　　　　　　　　SD345
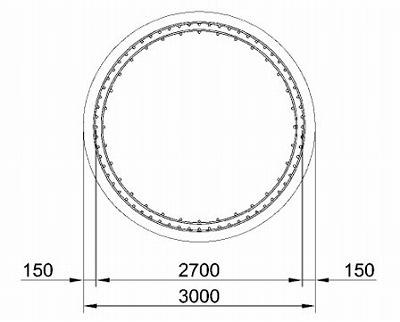
　直径　　　　　　　　　　3m
　軸方向鉄筋　　　　　　　D32
　芯かぶり　　　　　　　　150mm
　横拘束筋　　　　　　　　D19
　横拘束筋間隔　　　　　　150mm
　橋脚高さH　　　　　　　 10m
　慣性力作用高さh　　　　 10ｍ
　上部構造死荷重　　　　　5338kN
　単位体積重量　　　　　　24.5kN/m³
　橋脚死荷重　　　　　　　1732kN
　軸応力　　　　　　　　　1N/mm²

・次に塑性ヒンジ長を算出します。
　Lp=9.5σsy^1/6βn^-1/3φ'　≦0.15h
　Lp：塑性ヒンジ長（mm）
　σsy：軸方向鉄筋の降伏点（N/mm²）
　βn：軸方向鉄筋のはらみ出し抵抗ばね定数（N/mm²）
　h：橋脚基部から慣性力作用位置までの高さ（mm）
　βn=βs+βco
　βs：横拘束筋抵抗ばね定数（N/mm²）
　βs=(384×E₀×I_h)/(n_s×d'³×s)
　E₀：横拘束筋のヤング係数（N/mm²）
　I_h：横拘束筋の断面二次モーメント（mm⁴）
　d'：横拘束筋の有効長（mm）
　　　慣性力の作用方向と平行な横拘束鉄筋によって分割されたコンクリート部分の中で最も大きい値
　　　※円形断面の場合には最外縁の横拘束筋が囲むコンクリート直径の0.8倍の値とする
　n_s：横拘束筋の有効長d'が最も大きいコンクリート部分に配置される圧縮側軸方向鉄筋の本数
　s：横拘束筋の間隔（mm）
　βco：かぶりコンクリートの抵抗ばね定数（N/mm²）
　βco=0.01C₀
　C₀：横拘束筋の有効長d'が最も大きいコンクリート部分に配置される軸方向鉄筋の純かぶり（mm）
　φ'：横拘束筋の有効長d'が最も大きいコンクリート部分に配置される軸方向鉄筋のうち、
　　　小さい直径（mm）　40mm以上の場合は40mmとする

図-2　横拘束鉄筋図

　E₀=200000N/mm²
　I_h=6533mm⁴　　　　　　　横拘束筋直径=19.1mm
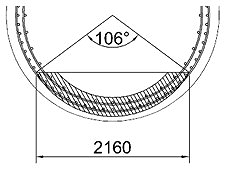
　d'=2160mm
　n_s=28本
　s=150mm
　βs=(384×E0×Ih)/(ns×d'³×s)
　　=0.012N/mm²
　C₀=134mm　　　　　　　　芯かぶり=150mm
　βco=0.01C₀
　　=1.34N/mm²
　βn=1.352N/mm²
　Lp=9.5σsy^1/6βn^-1/3φ'　　≦0.15h=1500mm
　　=724mm

・軸方向鉄筋の許容ひずみを算出します。
　εst2=0.025×Lp^0.15×φ^-0.15×βs^0.2×βco^0.22
　　=0.0175
　εst3=0.035×Lp^0.15×φ^-0.15×βs^0.2×βco^0.22
　　=0.0246
　εst2：耐震性能2の軸方向鉄筋の許容引張ひずみ
　εst3：耐震性能3の軸方向鉄筋の許容引張ひずみ
　φ：軸方向鉄筋の直径（mm）

・横拘束筋体積比を算出します。
　ρs=(4×Ah)/(s×d)
　　=0.00566
　ρs：横拘束筋体積比

・コンクリートの最大圧縮応力度に達する時のひずみを算出します。
　εcc=0.002+0.033β×(ρs×σsy)/σck
　　=0.00415
　εcc：コンクリートの最大圧縮応力度に達するときのひずみ
　β：断面補正係数　矩形断面：0.4　円形断面：1.0　　　 =1.0
　σsy：横拘束筋の降伏点（N/mm²）上限345N/mm²　　　=345N/mm²
　σck：コンクリートの設計基準強度（N/mm²）　　　　　=30N/mm²

・横拘束筋で拘束されたコンクリートの最大圧縮応力度を算出します。
　σcc=σck+3.8×α×ρs×σsy
　　=37.4N/mm²
　σcc：横拘束筋で拘束されたコンクリートの最大圧縮応力度（N/mm²）
　α：断面補正係数　矩形断面：0.2　円形断面：1.0 =1.0

・応力度-ひずみ曲線の下降勾配を算出します。
　Edes=11.2×σck² /(ρs×σsy)
　　=5163N/mm²
　Edes：応力度-ひずみ曲線の下降勾配（N/mm²）

・横拘束筋で拘束されたコンクリートの限界圧縮ひずみを算出します。
　εccl=εcc+0.5σcc/Edes
　　=0.00777

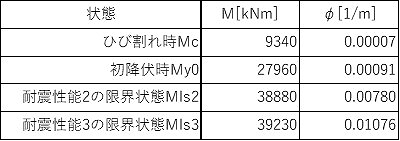
・曲げモーメントと曲率の算出
　以上のパラメータより算出した曲率が道路協会の計算例では以下のようになっています。

２．midasCivil（円形）
　ここからはmidasCivilのM-φ計算機能を使用してみます。
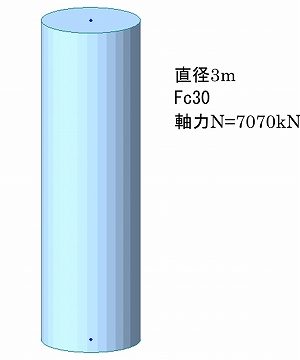
　まず、柱要素で計算するために図-3に示すように計算例と同断面（直径3m）、材料はFc30の鉛直要素を作成します。
　軸応力が1N/mm²となるように「初期断面力」を用いて7070kNを与えます。

図-3　計算要素図

　次にM-φパラメータを設定していきます。
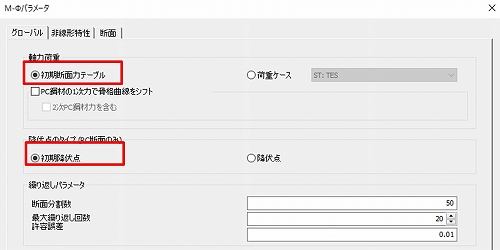
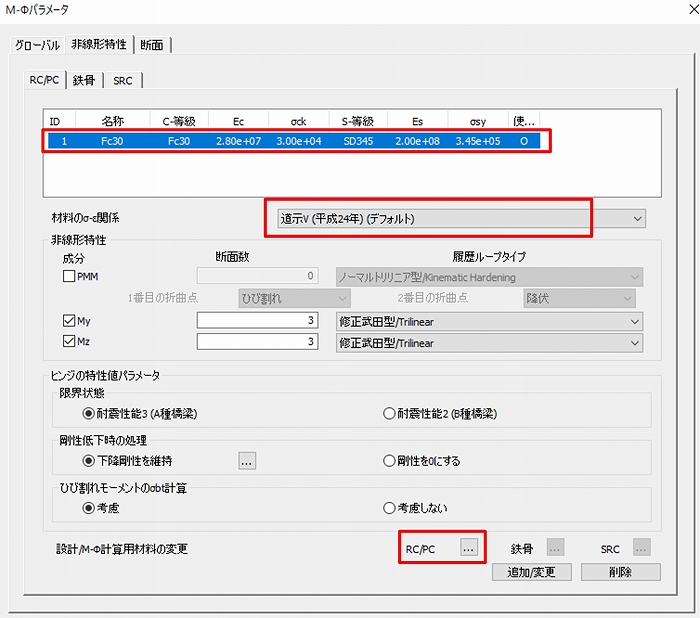
　図-4の「グローバル」タブでは軸力に「初期断面力テーブル」を選択し、降伏点のタイプは「初期降伏点」とします。

図-4　M-φグローバルデータ

　図-5の「非線形特性」タブでは「Fc30の行」を選択しσ-ε関係を「道示Ⅴ（平成24年）」とします。そして「RC/PC」のボタンをクリックして鉄筋の設定を行います。

図-5　非線形特性

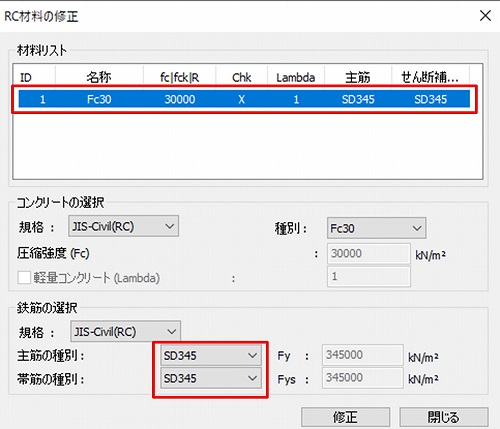
　図-6のRC材料の設定で「Fc30の行」を選択してから鉄筋の材料をSD345とします。

図-6　RC材料の修正

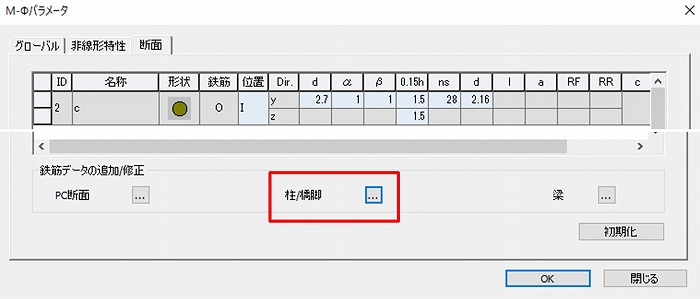
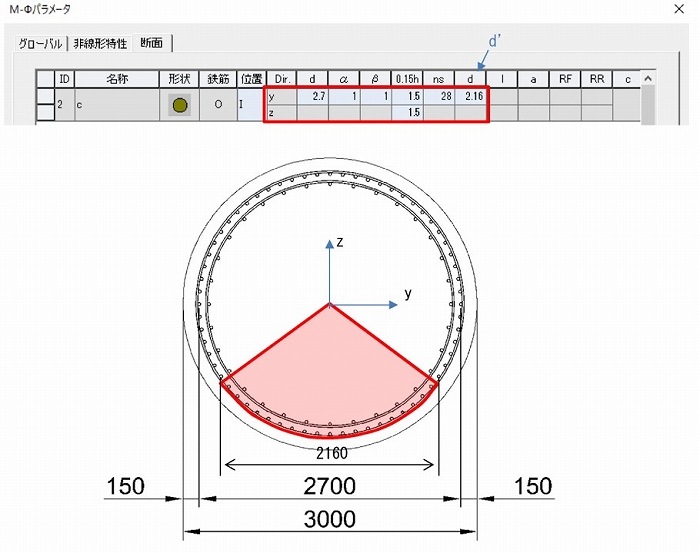
　次に図-7の「断面」タブですが、最初に「柱/橋脚」のボタンから鉄筋情報を入力します。

図-7　RC材料の修正

　図-8の鉄筋情報は該当断面を選択してから鉄筋データを入力します。
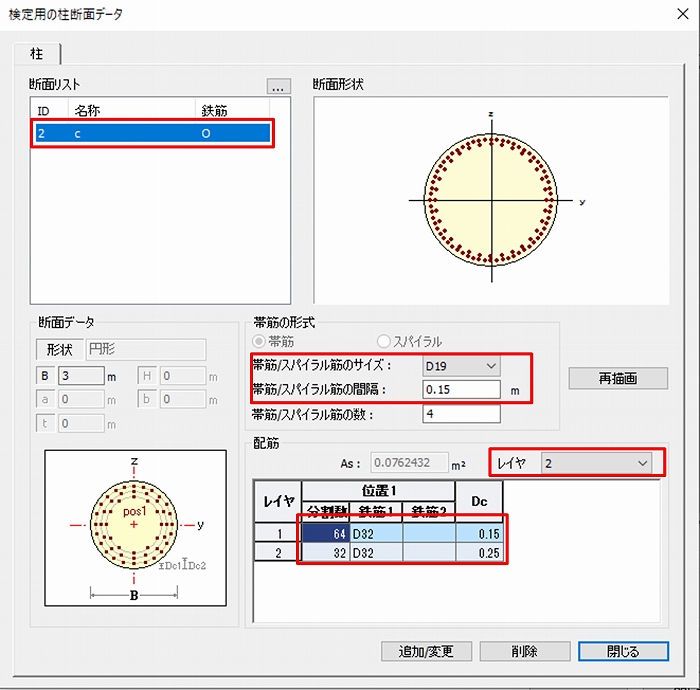
　帯筋にD19、間隔に0.15mとします。数は別途有効長を入力するので意味はなく適当な数字として下さい。
　主筋は2段目があるのでレイヤを2とし、鉄筋を入力します。「分割数」は本数のことで「Dc」がかぶりとなります。

図-8　鉄筋情報

　最後に図-9の「断面」タブで横拘束鉄筋パラメータを入力していきます。
　有効長dは2.7mとなります。ｄが2つありますが2つ目はd’であるため円形の場合は0.8dの2.16mとなります。
　α、βは円形の場合1.0となり、0.15hはｈ＝10mから1.5mとなります。
　横拘束筋に囲まれた圧縮鉄筋の本数nsは計算例と同じ28とします。

　以上の設定でM-φ計算を実行しますと要素にM-φパラメータが割り当てられます。
　割り当てられました数値と計算例の数値は以下のようになりました。

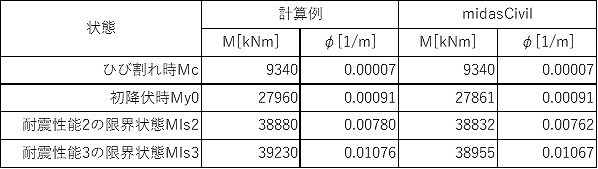
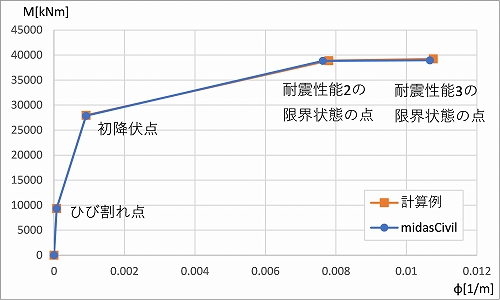
　モーメント、曲率ともに全て概ね一致する結果となりました。
　2024/4/23修正;midas Civil 2024 V1.1 (Ver.945)で修正されたことにより