RC床版にシェル要素を用いた非合成桁の再現解析
Civil Tips 2023.05.101.はじめに
今回は非合成桁とRC床版のモデル化について、実橋での載荷実験(写真参照)の結果との比較を交えて紹介します。
鋼非合成桁橋の数値解析では、主桁と床版の合成を考慮しない格子モデルを用いる場合も多いですが、実際には付着やスラブアンカー等により合成状態に近い挙動を示すため、活荷重応力は計算上過大評価されていると指摘されています。また、連続桁での実橋載荷試験結果を用いた非合成桁橋の挙動の再現事例は少ないため、床版をシェル要素でモデル化し、主桁と剛結することで合成状態を模擬し、実験結果の再現性を検討します。
詳細な解析のためには、全要素をシェル要素やソリッド要素で作成したモデルの使用も考えられますが、モデル化が高難度になることや解析時間が長くなってしまうこと等の理由で実用的とは言えません。本稿では主桁を梁要素で、その他の部材(対傾構等)をトラス要素でモデル化し、節点数や要素数を低減したモデルでの解析精度も確認したいと思います。
写真：実橋載荷実験の様子
2.対象橋梁
対象橋梁の諸元を以下に示します。
橋長 ： 55.5 m
支間長 ： 27.4 m + 27.4 m
形式 ： 2径間連続非合成鈑桁橋
供用年数 ： 約20年
設計荷重 ： A活荷重
床版 ： 鉄筋コンクリート 200 mm
舗装 ： アスファルト 50 mm
ずれ止め ： 丸鋼16 mmのスラブアンカーを橋軸方向に1 m間隔で配置
3.解析モデル
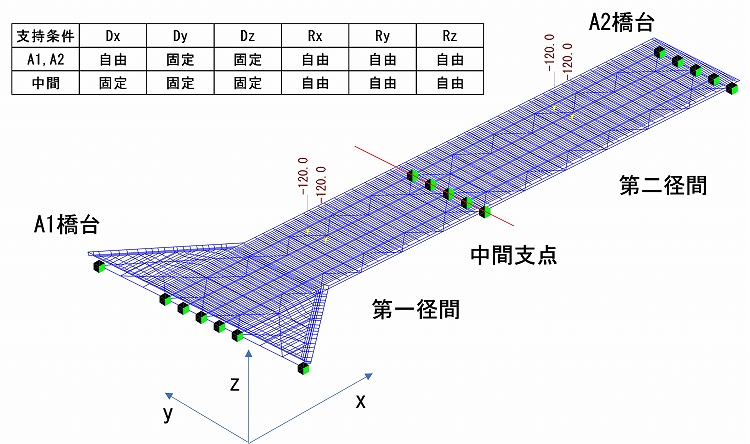
対象はG1からG5の5本の二径間連続鋼桁と拡幅部のG6,G7枝桁、RC床版で構成されています。
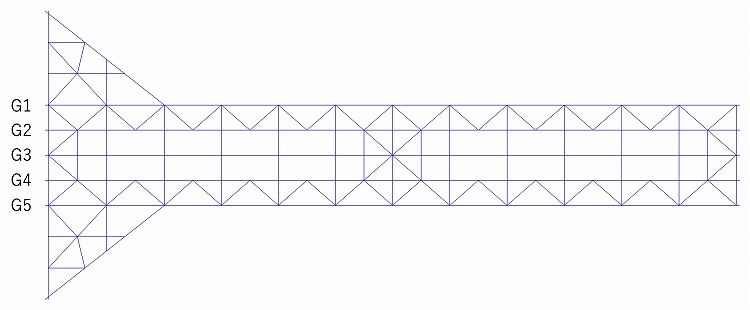
主桁と分配横桁には梁要素、そのほかの対傾構等の鋼製部材にはトラス要素を用いてモデル化します(図1)。主桁はウェブの高さの中点を基準として節点を設けます。
図1 梁要素・トラス要素(鋼部材)
床版は上面を基準とし、ハンチは簡単のため無視します。主桁上は300mm、それ以外は200mmの厚さをもつシェル要素でモデル化します(図2)。主桁の節点とその直上の床版の節点を剛結(剛体連結)することで合成状態を模擬します(図3)。
図2 シェル要素(床版)
図3 一般断面図
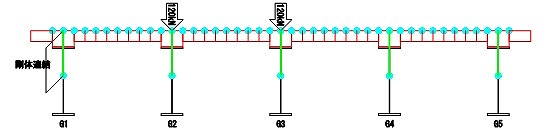
また地覆や舗装は剛性を考慮しないこととします。荷重は実験に合わせ、片輪あたり120kNをG2とG3上、応答が大きくなる各スパンの中央に載荷します(図4)。活荷重による影響を検討するため自重は考慮しません。
支持条件は、橋台A1、A2は可動支承、中間支点は固定支承なので、図4内の表に示した条件とします。
図4 荷重位置(kN) 支持条件
床版が実橋の厚さのモデル①(床版剛性あり)と、シェル要素の厚さを一律0.001mmとし、床版の剛性を見込まないモデル②(床版剛性無視)を作成し、比較しました。なお、床版の厚さ以外の条件は2モデル共通としています。
このように、シェル要素の厚さを変えることによって桁と床版の合成の影響を比較できるほか、主桁の軸線以外の位置に載荷する場合にも対応することができます。
*参考モデル
土木研究所資料「鋼桁橋の設計へのFEM解析の適用に関する研究」p.37-p.40
4.変位の比較
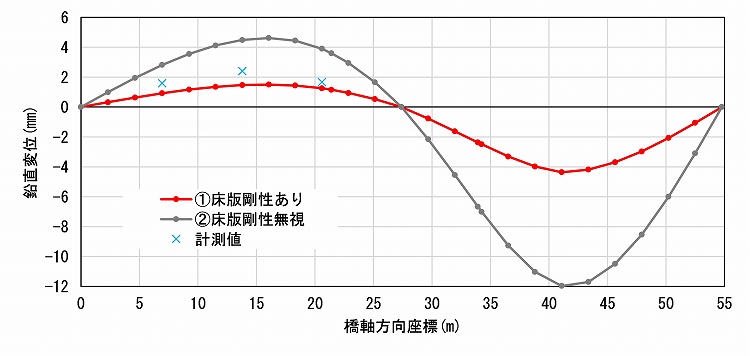
荷重直下のG2桁の鉛直変位を実験での計測値と比較しました。
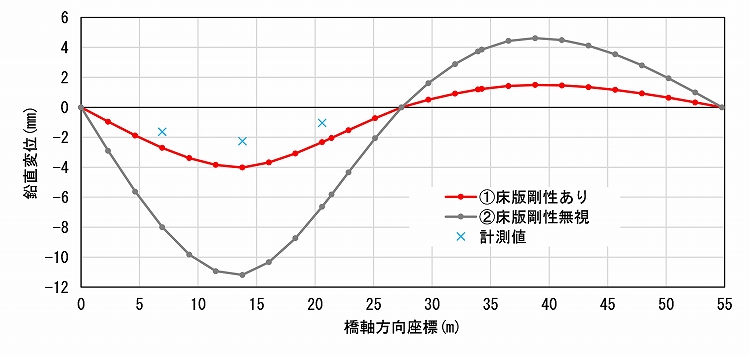
図5-1に示した第一径間への載荷時の変位の比較では、床版剛性を無視したモデル②の最大鉛直変位(約11.2mm)は計測最大値(約2.3mm)の約5倍と、過大評価しているのに対し、床版剛性を考慮したモデル①では計測値の約1.7倍(4.0mm)程度となっています。一般的に実構造物の材料強度は、解析で用いる公称値よりも大きいことを考えると、モデル①の解析では良好な精度の結果を得られたといってよいでしょう。
図5-1 第一径間載荷時鉛直変位(G2)
一方で第二径間へ載荷した際(図5-2)には、モデル①では上向きの最大変位(1.5mm)が計測値(2.4mm)より約40%小さく、モデル②では計測値の1.9倍(4.5mm)となりました。
実験状況により第二径間の変位は計測していませんが、活荷重による変位が上向きとなる、荷重位置の反対側の径間では鉛直変位の解析値が計測値より小さくなる可能性があります。また、実験では大型車両を用いて載荷を行っており、節点への集中荷重による解析とは必ずしも一致しないという点を踏まえ、大小関係についてはさらに検討する必要がありますが、精度としてはモデル①がより計測値に近い結果となりました。
図5-2 第二径間載荷時鉛直変位(G2)
5.応力度の比較
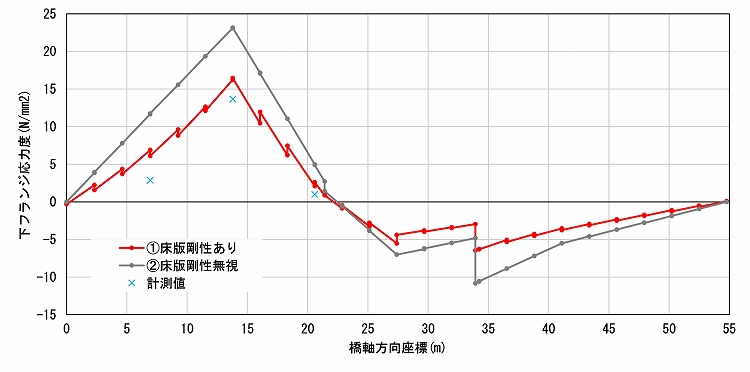
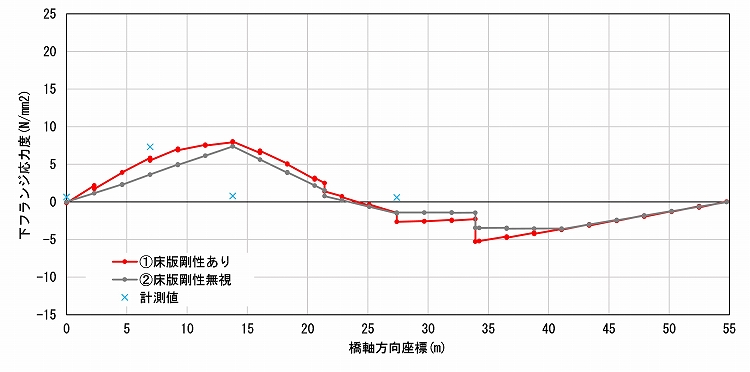
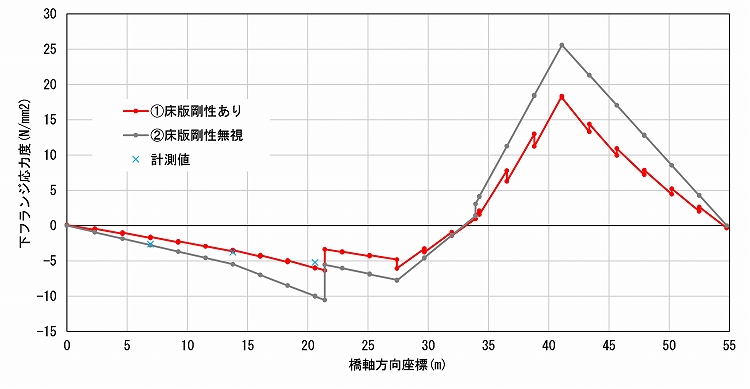
荷重直下のG2桁と荷重から最も離れたG5桁の応力度を、実験で計測したひずみをもとに鋼材のヤング係数2.0×10^5N/mm2で除して求めた応力度と比較します。
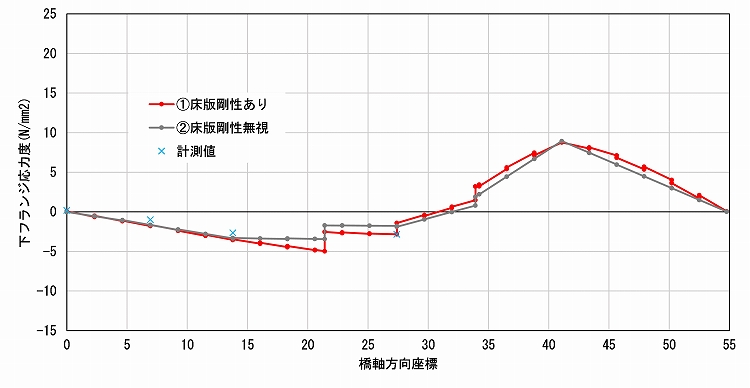
図6と図7に示した応力度の比較でも、実験値と近い値となっているのはモデル①です。モデル①ではG2の応力度が抑制されている一方、G5の応力度はモデル②よりわずかに大きくなっています。つまり、モデル①は橋軸直角方向に、より多く応力が伝達され、床版を含む全体で分担しているといえます。床版のシェル要素がある程度の応力を分担していることは、モデル①のグラフの不連続性からも読み取れます。
図6-1 第一径間載荷時応力度分布(G2)
図6-2 第一径間載荷時応力度分布(G5)
第二径間への載荷時には、応力度の大きい箇所で比較するとG2の計測値-5.21N/mm2との差がモデル①：3％(-6.03N/mm2)、モデル②：90%(-9.97N/mm2)(図6-1)、G3の計測値-2.84N/mm2との差はモデル①：0.1%(-2.84N/mm2)、モデル②：37.3%(-1.78N/mm2)(図6-2)となっており、特にモデル①で非常に高い精度の結果が得られました。
図7-1 第二径間載荷時応力度分布(G2)
図7-2 第二径間載荷時応力度分布(G5)
6.まとめ
非合成桁橋について、①床版の剛性を考慮する場合(すなわち床版と桁が合成していると考える場合)と②しない場合を比較し、概して①のモデルが、より実現象に近い結果を得られることがわかりました。非合成桁であっても合成作用を考慮できるモデルで解析すべきであるといえます。
また、桁を梁要素としてモデル化を容易にした場合でも十分に制度の良い結果が得られることが分かりました。難度を下げたモデルを用いることで、供用中の橋梁の応力状態を効率的に評価することができ、その後の維持管理の合理化が期待できます。
連続桁としての挙動は、合成状態の模擬によって精度が高まりましたが、活荷重によって上向きの変位となる箇所について、解析結果と計測結果の大小関係が他のケースとは異なる傾向となったため、引き続き検討を進めていきたいと思います。
参考文献
土木研究所「鋼桁橋の設計へのFEM解析の適用に関する研究」2007年
土木学会「モニタリング技術活用のための指針(案)」2022年