１．はじめに
　基礎構造物には土圧，地震力や波力などにより，鉛直荷重Vに加えて水平荷重HやモーメントMが作用します。組合せ荷重を受ける直接基礎の支持力解としては，これまでにHansenやMeyerhofなどによる慣用的な手法が提案されています。ここでは、偏心荷重が作用する剛な円形直接基礎における支持力曲線の適用性について，既往の提案式と室内実験結果を比較したので報告します。

２．支持力曲面について
　図-1に（V，H，M）空間あるいは無次元化した（V/V₀，H/V₀，M/RV₀）空間における支持力曲面の一例を示します。ここでV₀は、鉛直力Vのみが作用する場合（H=M=0）での最大鉛直荷重です。直接基礎の支持力曲面はラグビーボールのような形状を有しており，降伏曲面（あるいは塑性ポテンシャル）としてもみなせる可能性があります。

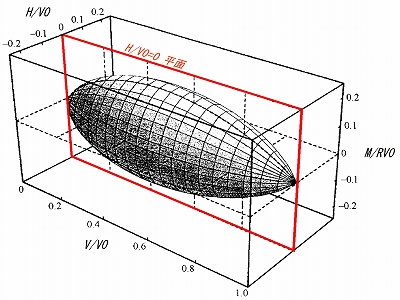
図-1　直接基礎の支持力曲面の例

　傾斜荷重（水平荷重H）が作用せずに偏心荷重（V，M）のみを受ける場合は，図-1の支持力曲面においてH/V₀0＝の平面で切断した断面が2次元の支持力曲線として表現されます。ちなみに支持力曲線は前述した慣用的な手法（静力学的公式）とは異なり，実験結果を基に得られているため，杭材の終局M－N関係とは性質が若干異なります。

３．偏心荷重時における支持力曲線
　Sekiguchi，HoulsbyおよびMeyerhofらは，偏心荷重時（V，M，H=0）における円形直接基礎の支持力曲線として，下式を提案しています^1),2)。

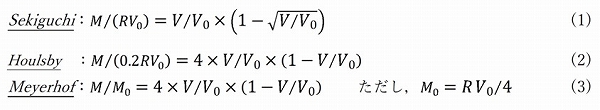
　ここでRは円形基礎の半径，（V，M）および（V₀，M₀）は，それぞれ偏心量e≠0およびe＝0における最大鉛直荷重および最大モーメントを表しています。なお，(3)式は偏心荷重時における有効載荷半径R‘＝R－e＝R－M/Vを，実務において一般的に用いられているMeyerhofの支持力式に適用することにより得ることができます。

４．支持力曲線と室内実験結果の比較
　図-2に(1)～(3)式から得られる鉛直荷重とモーメントに関する支持力曲線［V/V₀～M/RV₀］，およびGeorgiadis³⁾らによって得られた直接基礎の室内実験結果を示します。図-2より本ケースにおいては，Tresca材料（γ=φ=0°，c）において下界値として求められたSekiguchiの式は小さめ，Meyerhofの式は大きめ，Houlsbyの式はそれらの中間程度の支持力を与えていることが認められます。全般的にばらつきがあるものの，支持力曲線（(1)～(3)式）と室内実験結果の整合性は，おおむね良好であると考えられます。

図-2　支持力曲線と室内実験結果の比較

５．おわりに
　本報告では既往の支持力曲線の提案式と模型実験結果の比較を行い、当該ケースにおいては両者は大まかに一致する結果が得られました。今後は、傾斜荷重時（V，H，M=0）や基礎の根入れ効果の影響などについても検討を行う予定です。

【参考文献】